智能电机的 PMSM 参数识别
永磁同步电机 (PMSM) 由于其高效率、高功率密度和出色的机械动力性能而广泛应用于工业领域。PMSM通常采用磁场定向控制 (FOC,也称矢量控制)来驱动,以提升其动态响应并能 充分利用电机潜力。PMSM 矢量控制包含电流环,速度环和位置环。为了实现最佳性能的控制设计,工程师需要精准的电机参数为 PMSM 控制系统建立适当的机械和电气数学模型。
数据手册并不总是可以获得,即使有,通常也不会涵盖每台电机面对的工作条件。本文将介绍一种识别 PMSM 参数的简单方法,它利用 MPS的智能电机控制模块解决了这个难题。这种智能电机基于带遗忘因子的递归最小二乘 (RLS) 算法,可以实时修改和监测 PMSM参数的变化。
PMSM的磁场定向控制(FOC)
FOC 的基本思想是能够分别控制磁通量和扭矩,类似于控制直流电机的方式。根据 Clarke 和 Park 变换,同步旋转 Q-D 坐标系下的 PMSM 模型可以使用等式(1)、等式(2)、等式(3)和等式(4)来计算: $$v_{QS}=r_S+ω_Rλ_{DS}+ρλ_{QS}$$
$$v_{DS}=r_{S}-ω_rλ_{QS}+ρλ_{DS}$$
$$λ_{QS}=L_Si_{QS}+L_Mi_{QR}$$
$$λ_{DS}=L_Si_{DS}+L_M i_{DR}$$ 其中下标 Q 和 D 分别表示 Q 轴和 D 轴变量, LS为电机自感,LM为电机互感。
为了进一步简化控制,转子磁通应在 D 轴上对齐,而 Q 轴上的转子磁通为零。Q 轴和 D 轴的磁通量可以分别用等式 (5) 和等式 (6)来估算:
$$λ_{QS}=L_Si_{QS}$$
$$λ_{DS}=L_Si_{DS}+λ_M^{''''}$$ 电磁扭矩可以用公式(7)来计算: $$T_E= frac {3} {2} frac {P}{2} (λ''''_{M}i_{QS} + (L_{D} - L_{Q}) i_{DS}i_{QS}) $$
遵循上述方程的转换步骤,磁通量可以直接由 D 轴电流控制。采用恒定的IDS,可以通过调节 Q 轴电流直接控制扭矩 (TE)。 如果IDS= 0,则电磁扭矩与IQS成正比。 通过上述推导,我们可以得出PMSM的FOC原理图(见图 1)。
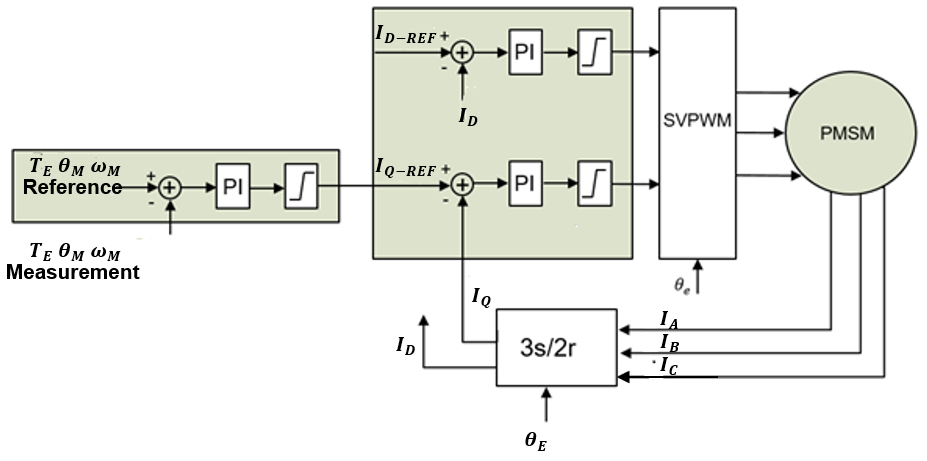
图 1:PMSM 矢量控制原理图
外环参考值可以是所需的扭矩、电机速度或特定的轴位置。将外环参考值与测量值进行比较,并将误差馈入控制器(通常为 PI 控制器)以生成扭矩电流参考值 (IQ-REF)。
D 轴电流参考值 (ID-REF) 根据磁通量要求来设置。电流调节器/控制器的输出(VQ-REF和VD-REF)为空间矢量 PWM (SVPWM) 的输入。SVPWM 模块为逆变器生成栅极信号以驱动 PMSM。
为实现 PMSM 伺服电机所需的动态性能,MPS的智能电机控制模块可以提供参数自整定功能,而且可以根据给定的带宽要求自动调整每个 PI 控制器。
对于电流环,开环传递函数可以用公式(8)来估算: $$G = frac{KPS+KI} {S} frac {1}{L_{S}S + r_S}$$
对于给定电流带宽S =jω,可以根据定子电阻和电感反向计算出PMSM 控制参数(KP 和 KI)。
与电流环类似,外环(机械环)开环函数可以用公式(9)计算: $$G = frac{KPS+K1} {S} frac {kt}{JS + B}$$
其中 kt 为电机扭矩常数,J 为惯量,B 为摩擦系数。
从等式 (9) 可知,已知电机扭矩常数 (kt)、惯量 (J) 和摩擦系数 (B),可以计算出外环的控制参数。
递归最小二乘算法
递归最小二乘算法 (RLS) 是最小二乘 (LS) 回归算法的递归应用,从每次迭代中获取新数据以修改系统先前的估值。
系统输出 (y(t)) 可以用公式 (10) 来计算: $$y(t)=?^T (t)θ(t)$$ 其中 ? 是系统输入矩阵,θ 是 PMSM 系统参数。
用$hat θ$ (这个符号请copy 英文原文字母) 表示估算的系统参数。目标函数,或旨在最小化或最大化的项,可以用等式 (11) 来估算:
$$J(θ,t)= frac {1}{2} ∑_{i=1}^t(y(i)-phi^T (i) hatθ (i)) $$ P 和 L 的新矩阵可以分别用等式 (12) 和等式 (13) 来计算: $$P^{-1}
(t)=∑_{i=1}^tphi(i)phi^T(i)$$ $$L(t)=P(t)phi(t)$$
递归最小二乘参数识别方案通过等式(14)、等式(15)、等式(16)、等式(17)和等式(18)估算: $$?(t)=(y(t)-phi^T (t)) hatθ (t-1)$$
$$L(t)=P(t-1)phi(t) (I+phi^T (t)P(t-1)phi(t))^{-1}$$
$$P(t)=(I-L(t)phi^T (t))P(t-1)$$
$$hatθ(t)=hatθ (t-1)+L(t)?(t)$$
$$t=t+1$$
在算法中添加一个遗忘因子能够使方案得以处理时变系统。根据数据的新旧,赋予遗忘因子数据以一定的权重。因为旧数据对当前迭代的影响较小,所以给最新数据赋予算法的最大权重。遗忘因子 (λ) 的取值范围在 [0,1] 之间。新的目标函数可以用等式(19)来估算:
$$J(θ,t)=frac {1}{2} ∑_{i=1}^tλ^{t-i} (y(i)-phi^T (i)hat θ (i)) $$
使用方程 (19) 中的新目标函数,第 n 个旧数据的权重为 λn。带遗忘因子的递归最小二乘方案可以通过等式 (20)、等式 (21)、等式 (22)、等式 (23) 和等式 (24) 来计算:
$$ ?(t)=(y(t)-phi^T (t)) hatθ (t-1)$$
$$L(t)=P(t-1)phi(t) (λI+phi^T (t)P(t-1)phi(t))^{-1}$$
$$P(t)= frac {1}{λ}(I-L(t) phi^T (t))P(t-1)$$
$$hatθ (t)=hatθ (t-1)+L(t)?(t)$$
$$t=t+1$$
实验结果
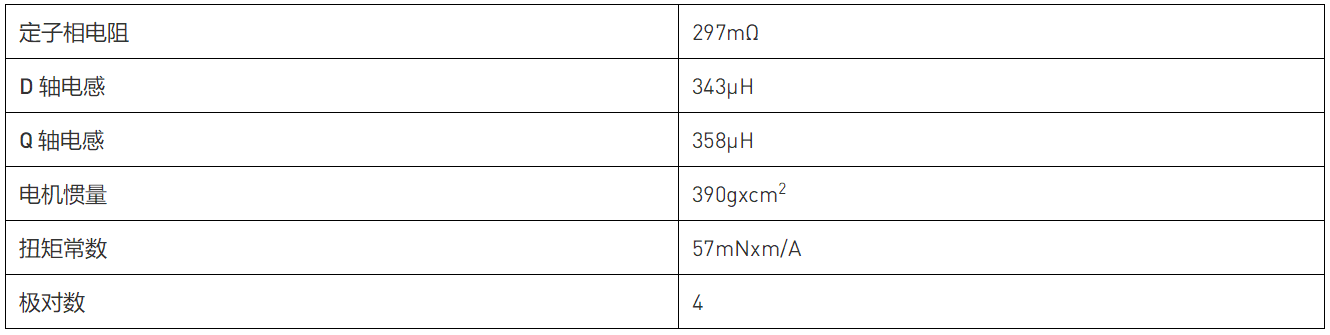
MPS’s MMP757188-36 是一款已经过验证的 智能电机。表 1 列出了其数据手册中的电机参数。
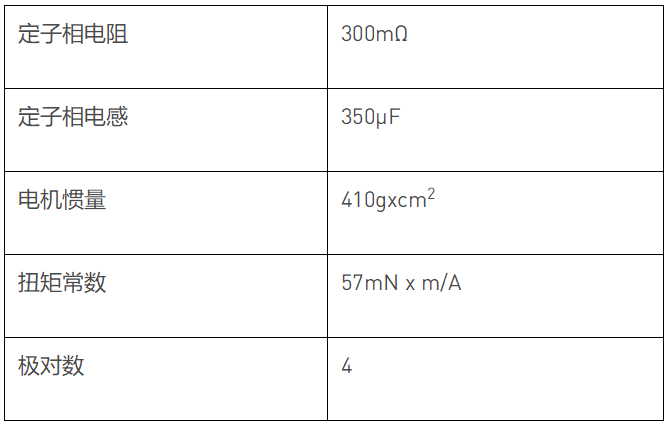

图 2:MPS 智能电机(MMP757188-36)
将以下电机参数的初始起点设置为[0 0 0 0 0]T: 相电阻(RS),Q轴电感(LQ),D轴电感(LD),扭矩常数(kt), 和电机轴惯量(J).
对于 RLS 算法,初始 P 矩阵设置为P = 10000 x I5 x 5,遗忘因子设置为 λ = 0.99.
将启动条件应用到 MPS 智能电机控制模块,执行 RLS 电机参数算法。图 3、图 4、图 5、图 6 和图 7 显示了其硬件实验结果。
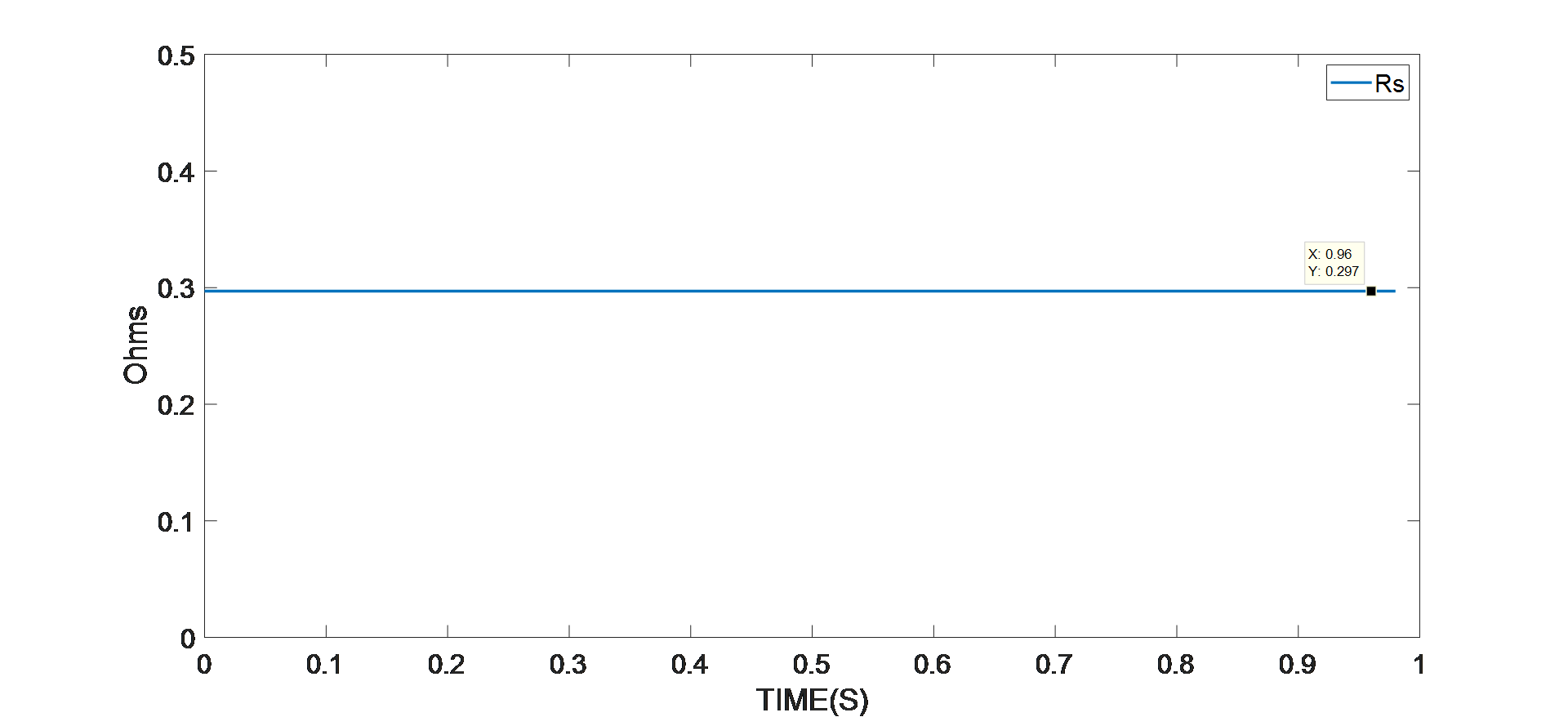
图 3:电阻识别的实验结果
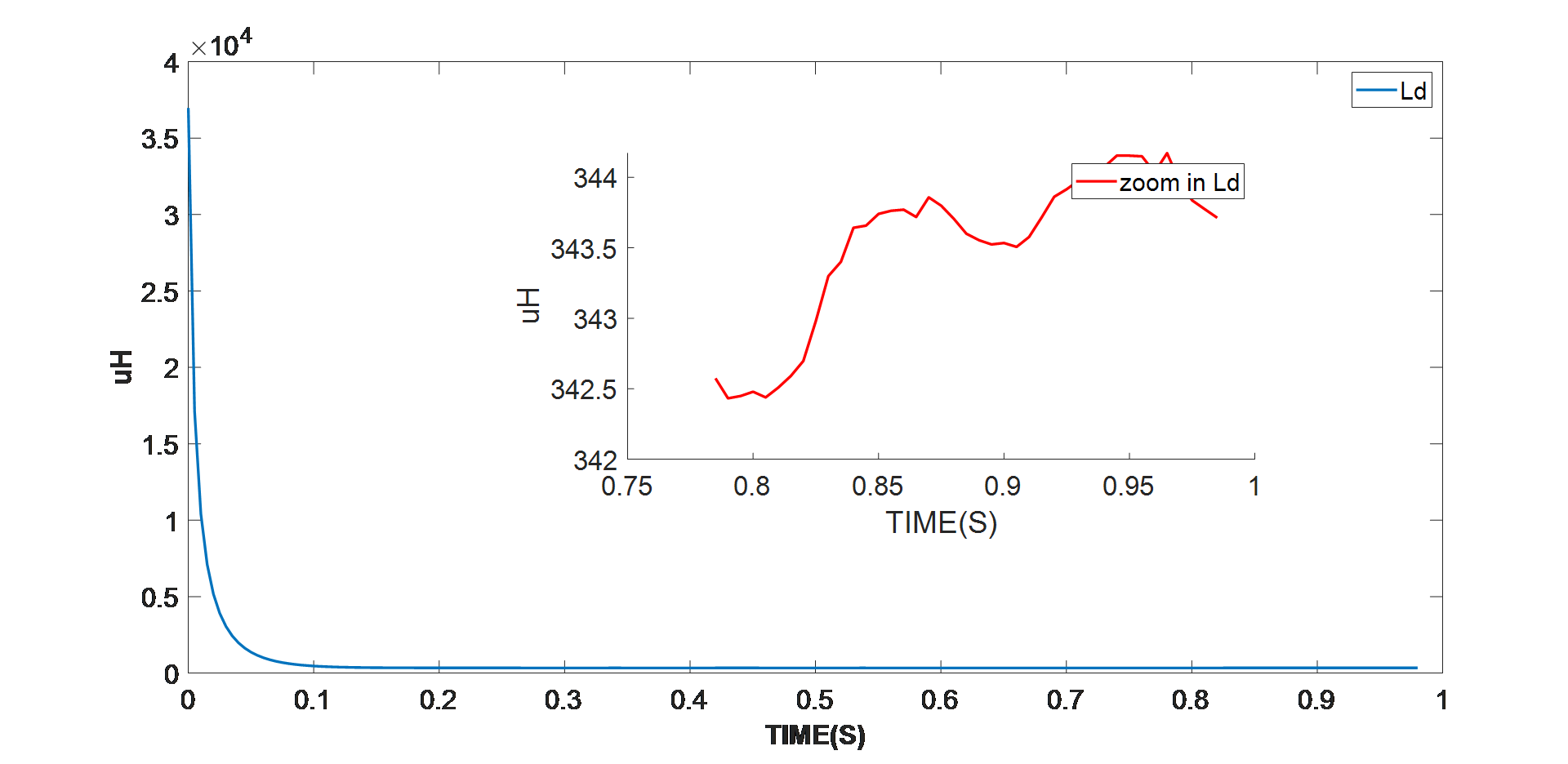
图 4:D 轴电阻识别的实验结果
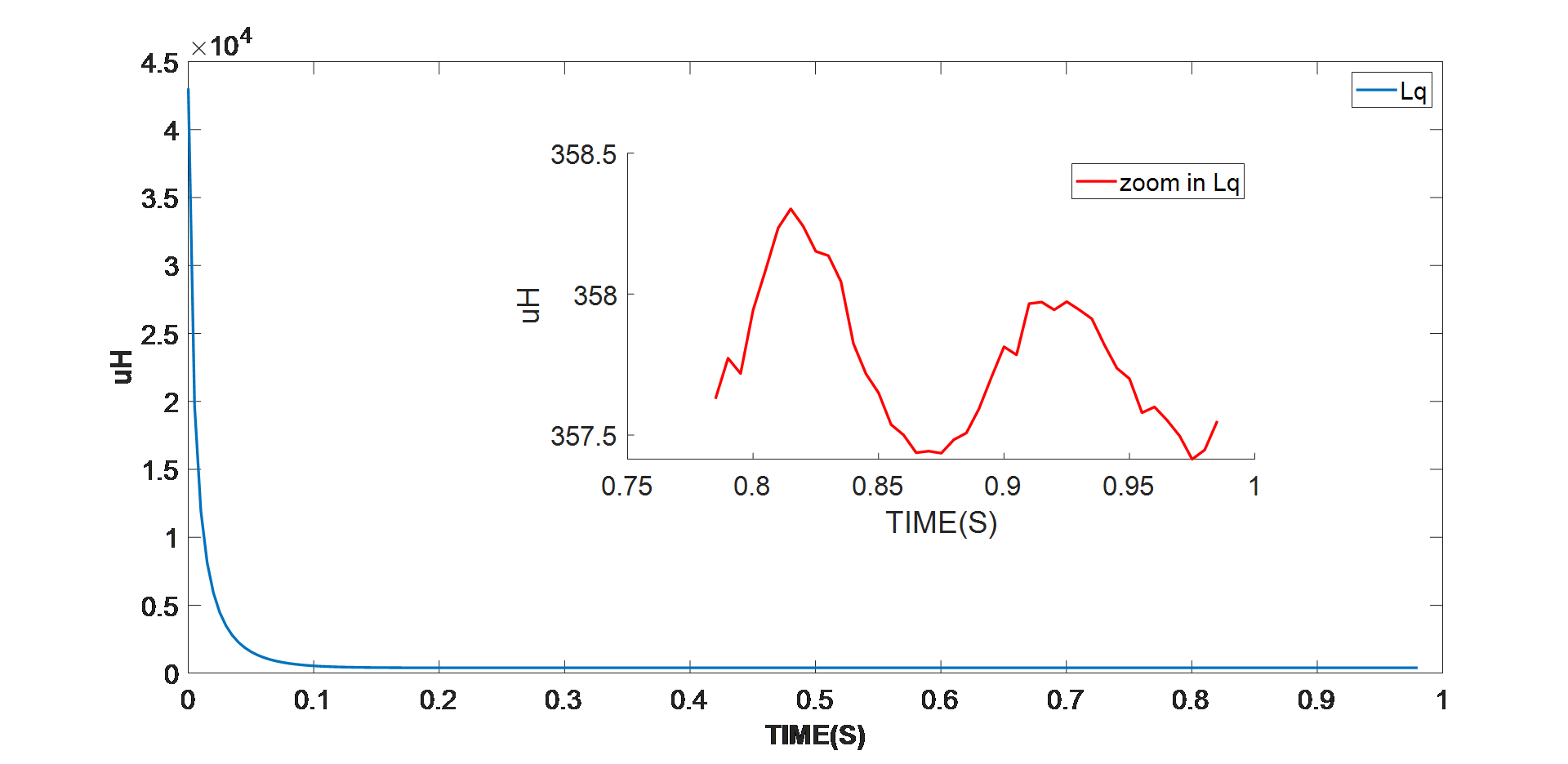
图 5:Q 轴电阻识别的实验结果
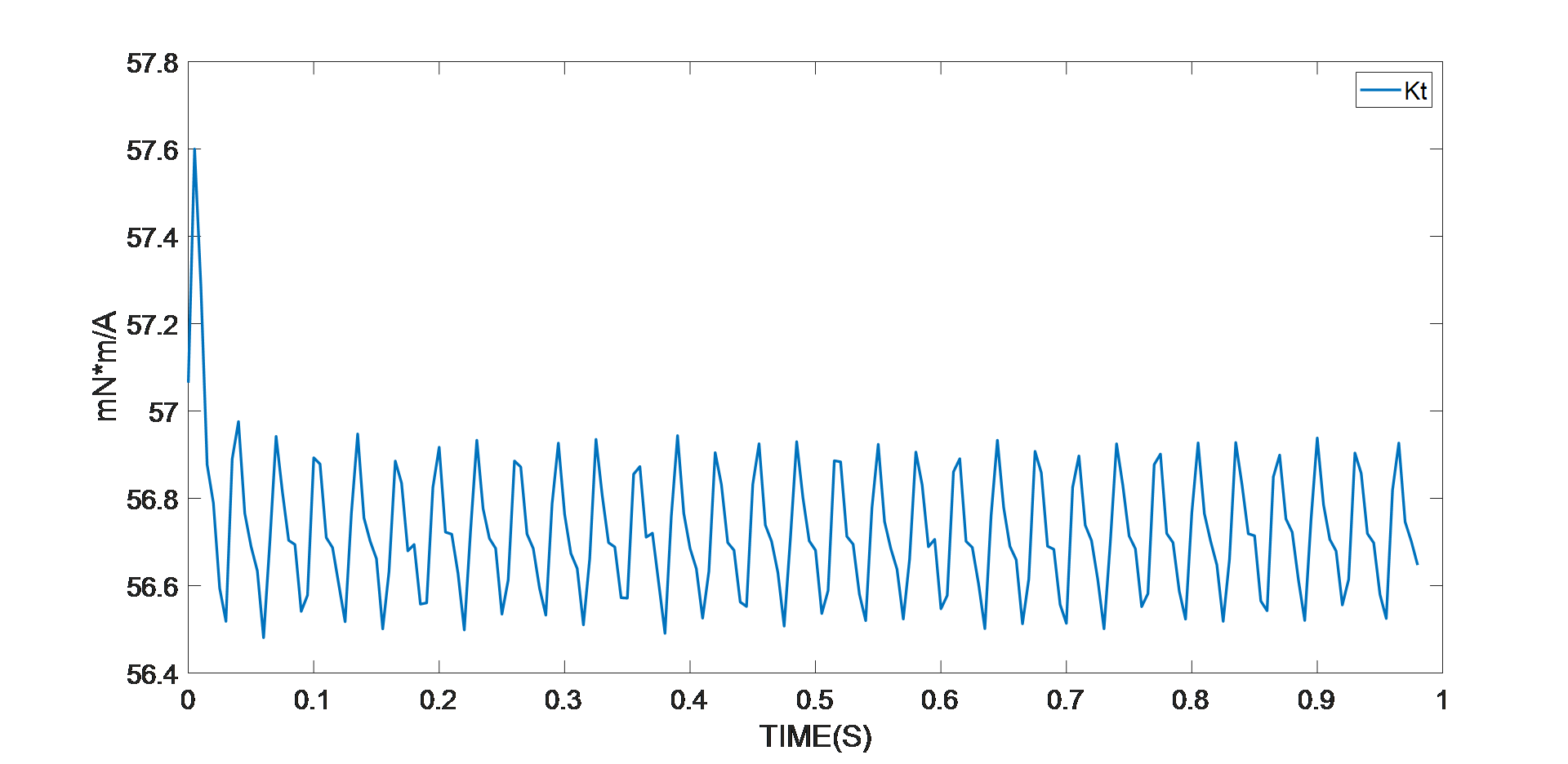
图 6:扭矩常数识别的实验结果
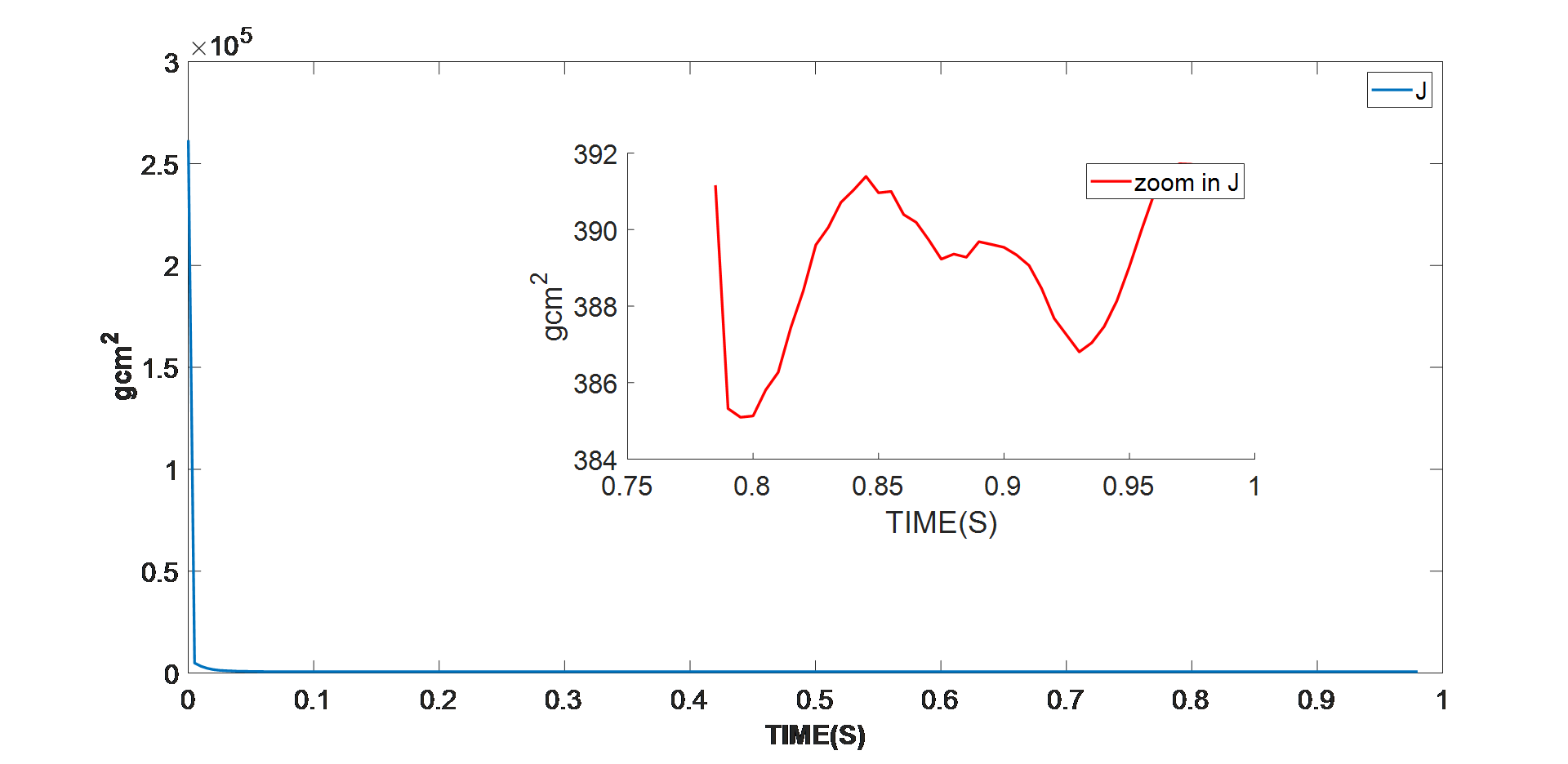
图 7:轴惯量识别的实验结果
智能电机控制模块(本例中为 MMP757188-36)检测参数识别算法是否已进入稳定阶段。如上图所示,在算法进入稳定状态之后,采用最终值,即平均电机参数值。
控制环自整定
如前文所述,电机参数会影响 PMSM 的 FOC 控制参数。为帮助工程师实现所需的电机性能,MPS 控制套件配备了智能电机控制模块,该模块使用公式 (8) 和公式 (9) 中得到的系统传递函数自动调整控制参数。如果已知电机参数,工程师只需通过 MPS eMotion GUI 为每个环路输入所需的带宽。上位机计算电机的控制参数,然后将控制参数反馈给智能电机以确保其性能。
PMSM 的控制传递函数高度依赖电机参数。如果电机参数不正确,电机将无法有效运行。在下面关于改变轴惯量 (J) 的示例中,我们将进一步讨论这个问题。
PMSM 通常被用作高性能伺服电机。它们的工作条件视情况而异。工程师可能有准确的电机参数数据手册,也有可能需要手动测量电机参数。一旦将电机置于复杂的机械系统中,就很难再确定轴惯量。
MPS’s MMP757188-36可用于驱动旋转盘(见图 8)。旋转盘的轴惯量从410 gxcm2增加到 7100 gxcm2。FOC设计为位置带宽是20Hz,速度带宽是200Hz,电流带宽是2000Hz。

图8:智能电机驱动旋转盘
如果使用的电机参数来自设备的数据手册,自动整定算法会采用预期的环路带宽来设计控制环,但由于数据手册仅提供空载惯量,因此电机参数会出错。位置参考是斜率为 10rad/s 的斜坡参考。图 9 表明,当位置环失控时,位置反馈将有较大的振荡。
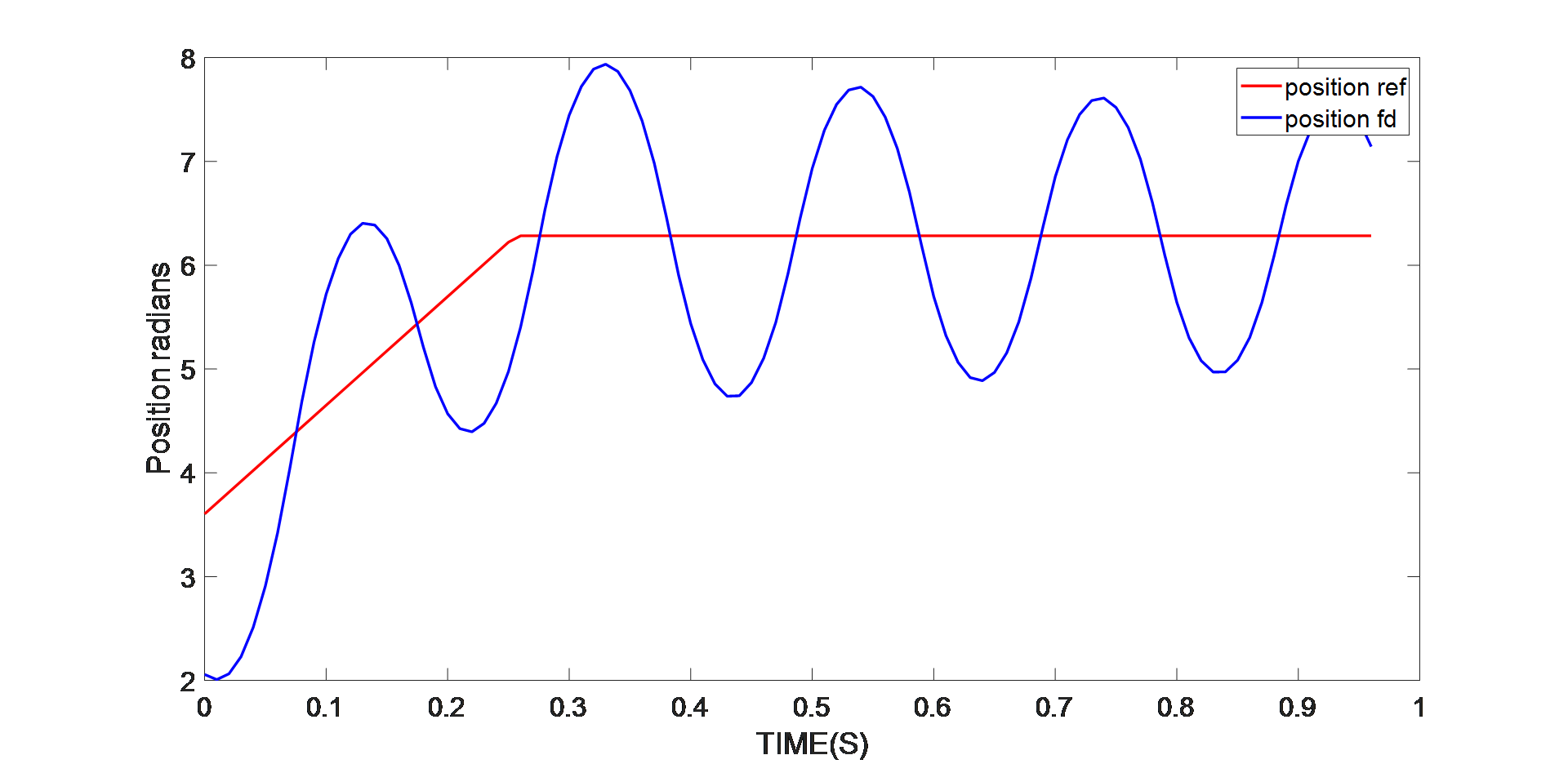
图 9:原始 J 值的位置控制性能
采用MPS的智能电机控制模块,运行参数识别算法。电机参数将根据电机当前工作条件更新,而自整定算法则能帮助工程师根据当前条件下的电机参数调整控制环路。电机使用相同的位置参考,位置反馈以 0.03% 左右的稳定误差追踪参考值(见图 10)。
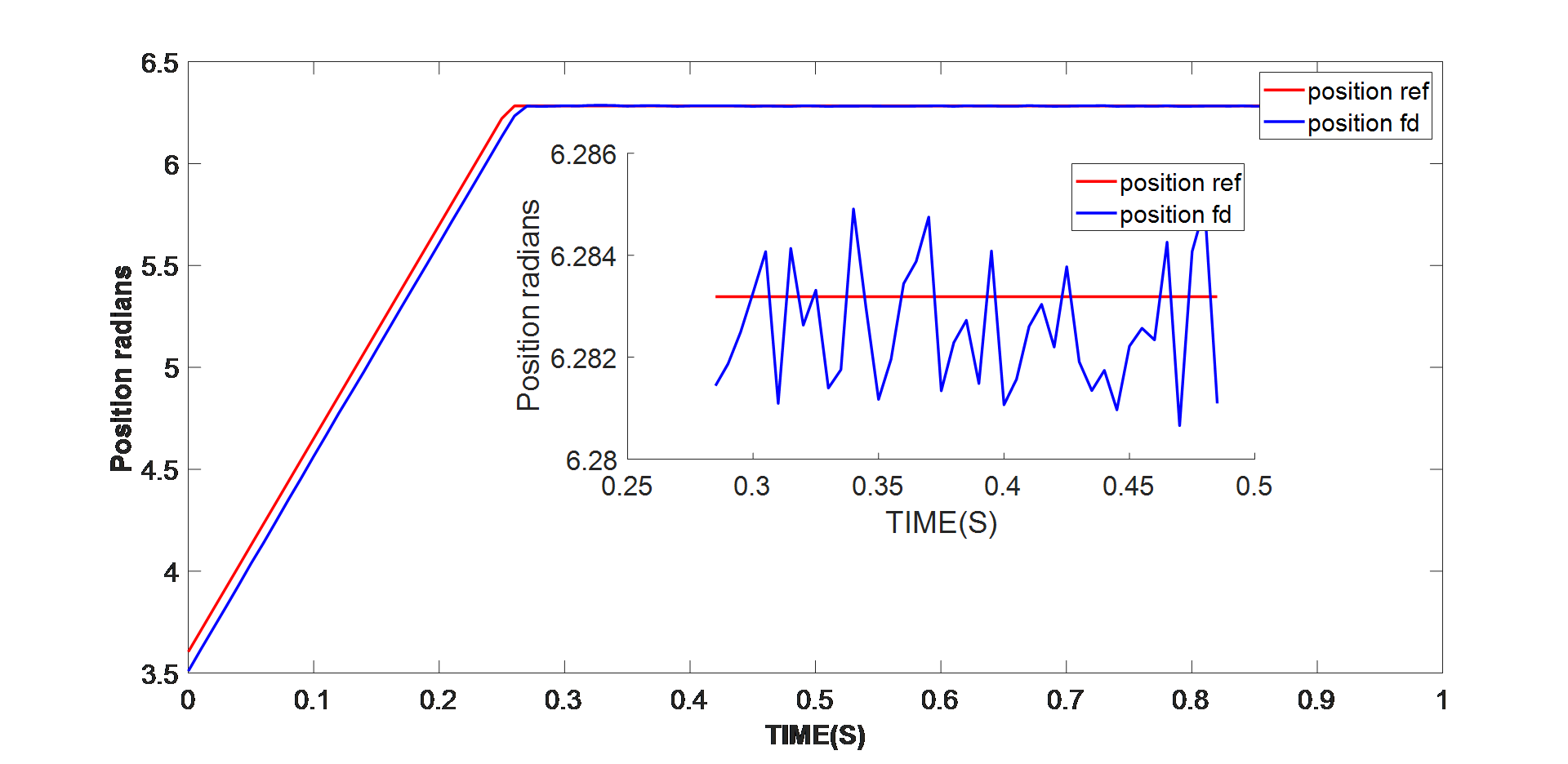
图 10:更新 J 值的位置控制性能
结论
本文介绍了如何利用MPS智能电机控制模块实现基于 RLS 的PMSM电机参数识别解决方案,并采用MPS 的 MMP757188-36在硬件实时测试中验证了其性能。文中还给出了具有不同惯量值的位置控制示例,用以说明参数识别的重要性。另外,由于PMSM FOC 取决于多个电机参数,本文还证明了其他参数对控制环路的影响。
