让你轻松理解天线驻波比!信号与频谱知识,都在这里了!
品慧电子讯电压驻波比(VSWR)是射频技术中最常用的参数,用来衡量部件之间的匹配是否良好。当业余无线电爱好者进行联络时,当然首先会想到测量一下天线系统的驻波比是否接近1:1, 如果接近1:1,当然好。常常听到这样的问题:但如果不能达到1,会怎样呢?驻波比小到几,天线才算合格?为什么大小81这类老式的军用电台上没有驻波表?
VSWR及标称阻抗
发射机与天线匹配的条件是两者阻抗的电阻分量相同、感抗部分互相抵消。如果发射机的阻抗不同,要求天线的阻抗也不同。在电子管时代,一方面电子管本输出阻抗高,另一方面低阻抗的同轴电缆还没有得到推广,流行的是特性阻抗为几百欧的平行馈线,因此发射机的输出阻抗多为几百欧姆。而现代商品固态无线电通信机的天线标称阻抗则多为50欧姆,因此商品VSWR表也是按50欧姆设计标度的。
如果你拥有一台输出阻抗为600欧姆的老电台,那就大可不必费心血用50欧姆的VSWR计来修理你的天线,因为那样反而帮倒忙。只要设法调到你的天线电流最大就可以了。
VSWR不是1时,比较VSWR的值没有意义
正因为VSWR除了1以外的数值不值得那么精确地认定(除非有特殊需要),所以多数VSWR表并没有象电压表、电阻表那样认真标定,甚至很少有VSWR给出它的误差等级数据。由于表内射频耦合元件的相频特性和二极管非线性的影响,多数VSWR表在不同频率、不同功率下的误差并不均匀。
VSWR都=1不等于都是好天线
影响天线效果的最重要因素:谐振
让我们用弦乐器的弦来加以说明。无论是提琴还是古筝,它的每一根弦在特定的长度和张力下,都会有自己的固有频率。当弦以固有频率振动时,两端被固定不能移动,但振动方向的张力最大。中间摆动最大,但振动张力最松弛。这相当于自由谐振的总长度为1/2波长的天线,两端没有电流(电流波谷)而电压幅度最大(电压波腹),中间电流最大(电流波腹)而相邻两点的电压最小(电压波谷)。
我们要使这根弦发出最强的声音,一是所要的声音只能是弦的固有频率,二是驱动点的张力与摆幅之比要恰当,即驱动源要和弦上驱动点的阻抗相匹配。具体表现就是拉弦的琴弓或者弹拨的手指要选在弦的适当位置上。我们在实际中不难发现,拉弓或者拨弦位置错误会影响弦的发声强度,但稍有不当还不至于影响太多,而要发出与琴弦固有频率不同的声响却是十分困难的,此时弦上各点的振动状态十分复杂、混乱,即使振动起来,各点对空气的推动不是齐心合力的,发声效率很低。
天线也是同样,要使天线发射的电磁场最强,一是发射频率必须和天线的固有频率相同,二是驱动点要选在天线的适当位置。如果驱动点不恰当而天线与信号频率谐振,效果会略受影响,但是如果天线与信号频率不谐振,则发射效率会大打折扣。
所以,在天线匹配需要做到的两点中,谐振是最关键的因素。
在早期的发信机,例如介绍的71型报话机中,天线电路只用串联电感、电容的办法取得与工作频率的严格谐振,而进一步的阻抗配合是由线圈之间的固定耦合确定死的,在不同频率下未必真正达到阻抗的严格匹配,但是实际效果证明只要谐振就足以好好工作了。
因此在没有条件做到VSWR绝对为1时,业余电台天线最重要的调整是使整个天线电路与工作频率谐振。
天线的驻波比和天线系统的驻波比
天线的VSWR需要在天线的馈电端测量。但天线馈电点常常高悬在空中,我们只能在天线电缆的下端测量VSWR,这样测量的是包括电缆的整个天线系统的VSWR。微信公众号:滤波器,当天线本身的阻抗确实为50欧姆纯电阻、电缆的特性阻抗也确实是50欧姆时,测出的结果是正确的。
当天线阻抗不是50欧姆时而电缆为50欧姆时,测出的VSWR值会严重受到天线长度的影响,只有当电缆的电器长度正好为波长的整倍数时、而且电缆损耗可以忽略不计时,电缆下端呈现的阻抗正好和天线的阻抗完全一样。但即便电缆长度是整倍波长,但电缆有损耗,例如电缆较细、电缆的电气长度达到波长的几十倍以上,那么电缆下端测出的VSWR还是会比天线的实际VSWR低。
所以,测量VSWR时,尤其在UHF以上频段,不要忽略电缆的影响。
不对称天线
我们知道偶极天线每臂电气长度应为1/4波长。那么如果两臂长度不同,它的谐振波长如何计算?是否会出现两个谐振点?
如果想清了上述琴弦的例子,答案就清楚了。系统总长度不足3/4波长的偶极天线(或者以地球、地网为镜象的单臂天线)只有一个谐振频率,取决于两臂的总长度。两臂对称,相当于在阻抗最低点加以驱动,得到的是最低的阻抗。两臂长度不等,相当于把弓子偏近琴马拉弦,费的力不同,驱动点的阻抗比较高一些,但是谐振频率仍旧是一个,由两臂的总长度决定。如果偏到极端,一臂加长到1/2波长而另一臂缩短到0,驱动点阻抗增大到几乎无穷大,则成为端馈天线,称为无线电发展早期用在汽艇上的齐柏林天线和现代的1/2波长R7000垂直天线,当然这时必须增加必要的匹配电路才能连接到50欧姆的低阻抗发射机上。
偶极天线两臂不对称,或者两臂周围导电物体的影响不对称,会使谐振时的阻抗变高。但只要总电气长度保持1/2波长,不对称不是十分严重,那么虽然特性阻抗会变高,一定程度上影响VSWR,但是实际发射效果还不至于有十分明显的恶化。
QRPer不必苛求VSWR
当VSWR过高时,主要是天线系统不谐振时,因而阻抗存在很大电抗分量时,发射机末级器件可能需要承受较大的瞬间过电压。早期技术不很成熟时,高VSWR容易造成射频末级功率器件的损坏。因此,将VSWR控制在较低的数值,例如3以内,是必要的。
现在有些设备具有比较完备的高VSWR保护,当在线测量到的VSWR过高时,会自动降低驱动功率,微信公众号:滤波器,所以烧末级的危险比20年以前降低了很多。但是仍然不要大意。
不过对于QRP玩家讲来,末级功率有时小到几乎没有烧末级的可能性。移动运用时要将便携的临时天线调到VSWR=1却因为环境的变幻而要绞尽脑汁。这时不必太丧气。1988-1989年笔者为BY1PK试验4W的CW/QRP,使用长度不足1.5米的三楼窗帘铁丝和长度为1.5米左右的塑料线做馈线,用串并电容的办法调到天线电流最大,测得VSWR为无穷大,却也联到了JA、VK、U9、OH等电台。后来做了一个小天调,把VSWR调到1,但对比试验中远方友台报告说,VSWR的极大变化并没有给信号带来什么改进,好像信号还变弱了些,可能本来就微弱的信号被天调的损耗又吃掉了一些吧。
总之,VSWR道理多多。既然有了业余电台,总是免不了和VSWR打交道,不妨多观察、积累、交流各自的心得吧。
天线系统和输出阻抗为50欧的发信机的匹配条件是天线系统阻抗为50欧纯电阻。要满足这个条件,需要做到两点:
第一,天线电路与工作频率谐振(否则天线阻抗就不是纯电阻);
第二,选择适当的馈电点。
一些国外杂志文章在介绍天线时经常给出VSWR的曲线。有时会因此产生一种错觉,只要VSWR=1,总会是好天线。微信公众号:滤波器,其实,VSWR=1只能说明发射机的能量可以有效地传输到天线系统。但是这些能量是否能有效地辐射到空间,那是另一个问题。一副按理论长度作制作的偶极天线,和一副长度只有1/20的缩短型天线,只要采取适当措施,它们都可能做到VSWR=1,但发射效果肯定大相径庭,不能同日而语。做为极端例子,一个50欧姆的电阻,它的VSWR十分理想地等于1,但是它的发射效率是0。 而如果VSWR不等于1,譬如说等于4,那么可能性会有很多:天线感性失谐,天线容性失谐,天线谐振但是馈电点不对,等等。在阻抗园图上,每一个VSWR 数值都是一个园,拥有无穷多个点。也就是说,VSWR数值相同时,天线系统的状态有很多种可能性,因此两根天线之间仅用VSWR数值来做简单的互相比较没有太严格的意义。 天线VSWR=1说明天线系统和发信机满足匹配条件,发信机的能量可以最有效地输送到天线上,匹配的情况只有这一种。 本文不打算重复很多无线电技术书籍中关于电压驻波比的理论叙述,只是想从感性认识的层面谈几个实用问题。
信号与频谱知识,都在这里了!
1 信号简介
信号(singal)简介
我们在生活中经常遇到信号。比如说,股票的走势图,心跳的脉冲图等等。在通信领域,无论是的GPS、手机语音、收音机、互联网通信,我们发送和接收的都是信号。最近,深圳地铁通信系统疑似与WiFi信号冲突,也就是地铁的天线收到了WiFi的信号,而误把该信号当作地铁通信信号。我们的社会信息化,是建立在信号的基础上的。
信号是随着时间或者空间变化的序列。在信号处理中,我们常用“信号”来特指一维信号,也就是只随单一一个时间或空间维度变化的序列,这样的信号在数学上可以表示成f(t)或者f(x)这样一个函数。与一维信号形成对应的是多维信号,比如说图像是二维信号,它随x,y两个空间维度变化,从数学上表示成为f(x, y)。下面在没有特别声明的情况下,都使用“信号”来代指一维信号。
尽管信号的使用如此广泛,但信号从数学意义上来并没有什么神秘的地方,只是普通的序列(函数)。信号处理的方法可以通用于任何一个领域的信号(无论是通信、金融还是其他领域),这也是信号处理的魅力所在。
2 简谐波
简谐波(simple harmonic)
正弦波(sine wave)和余弦波(cosine wave)统称为简谐波。简谐波是自然界最常见的波动。
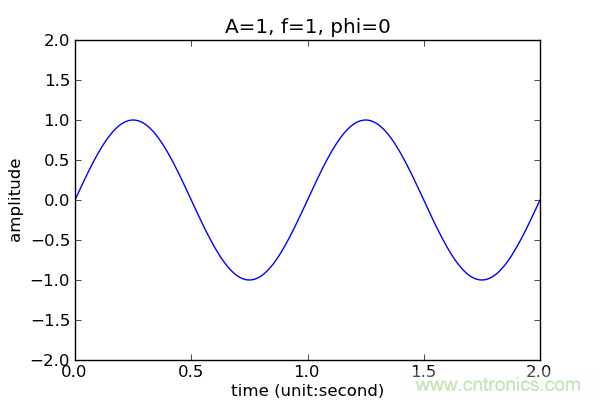
正弦波
正弦波可以写成函数的形式:
![]()
可以看到,一个简谐波三个参数,振幅(A, amplitude)、频率(f,frequency)、相位(phi, phase)。这三个参数分别控制正弦波的不同特征。通过调整它们,我们可以得到不同的正弦波信号。
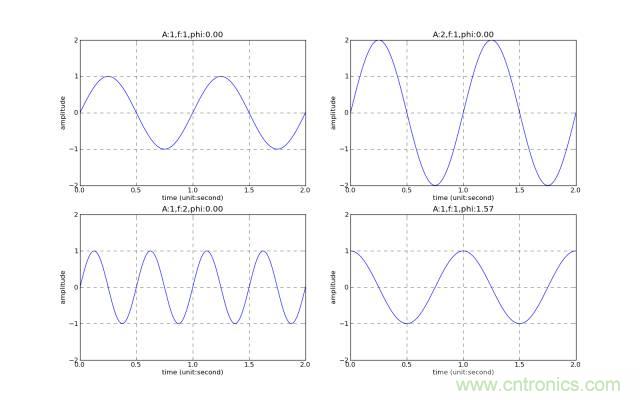
左上:原始 右上:2倍振幅
左下:2倍频率 右下:相位移动
可以看到,频率高,“山峰”越密集。振幅高,“山峰”越高。相位改变,“山峰”的位置左右移动。(朋友说我是"用音量控制音调":唱歌本应该改变频率高低的时候,却在改变振幅的高低。)
余弦波(cosine wave)函数形式与正弦波类似,用cos表示。我们可以通过改变正弦波来从正弦波获得余弦波。
3 傅立叶变换
傅立叶变换 (Fourier Transform)
简谐波虽然简单,但对信号处理具有重要意义。傅立叶是一名工程师,他发现,任何信号实际上都可以通过简谐波相加近似得到。也就是傅立叶定理(Fourier inversion theorem):任何一个信号都可以由简谐波相加得到。因此,复杂的信号可以分解成为许多个简单的简谐波。一个信号由多个频率的简谐波相加得到。组成信号的某个简谐波,称为信号的一个分量(component)。
比如下图,显示了我们如何用简谐波的叠加来不断趋近蓝色的信号:
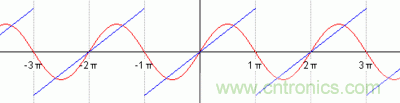
来自Wikipedia
傅立叶变换是一套固定的计算方法,用于算出信号的各个分量(也就是上面的an,bn)。在信号处理时,可以将信号进行傅立叶变换,转换为简谐波的组合。通过分别控制各个频率上的简谐波分量,我们可以更加有效的进行信号处理。比如说,我们通信的时候可以使用高频的简谐波信号。但是接收信号的天线可能会收到其他频率的干扰信号。这个时候,我们可以对接收到的混合信号做傅立叶变换,只提取目标高频的分量。这是降低信号噪音的常用方法。傅立叶变换的过程有些复杂,但已经有大量的程序可以帮你进行。你所需要的只是输入信号,计算机会帮你算出它的各个分量。
比如说,如果信号f(x)是周期性的,我们可以将它变换成:
![]()
也就是说,一个信号可以看做许多简谐波的和。上面的a,b是可以通过原信号求得的参数为:
![]()
![]()
a, b代表了信号在各个频率上的简谐波分量的强弱(以及相位)。这样,信号就分解为了简谐波的和。由于简谐波比较容易理解,我们可以通过研究这些分量,来明白复杂信号背后的机制。
4 频谱
频谱(frequency spectrum)
通过傅立叶变换,我们可以得到一个信号f(t)的不同频率的简谐波分量。每个分量的振幅,代表了该分量的强弱。将各个频率分量的强弱画出来,可以得到信号的频谱。比如下图是从每天降水序列中得到的频谱:
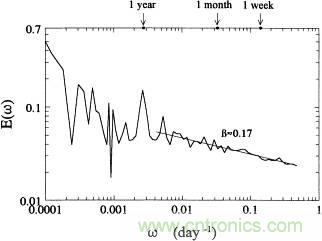
可以看到,以1年为周期的简谐波分量有一个明显的高峰。也就是说,一年周期的分量有比较强。这是有物理原因的。因为降水总是以一年四季为周期有规律的变化。通过信号->Fourier Transform->频谱,我们可以从简谐波分量的角度,理解复杂信号是由哪些简谐机制合成的。
图像处理(Image Processing)
傅立叶变换同样可用于多维信号。把傅立叶变换用于二维信号,即图像:
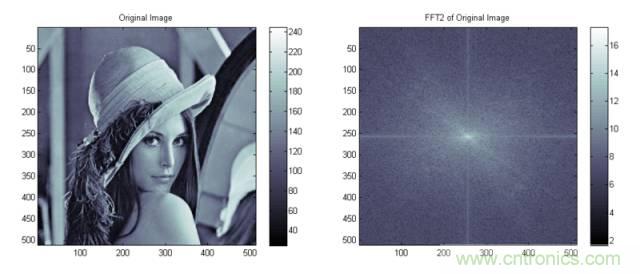
左边是二维信号(图像,f(x,y))。黑白可以用数值表示,即信号值。右边是二维图像的频谱。X轴表示x方向的频率,Y轴表示y方向的频率,黑白表示不同频率分量的振幅强弱。在下面一行中,Lenna被故意加上了噪声,并引起频谱的相应变化。频谱的中心代表了低频信号的振幅,频谱远离中心的地方代表了高频信号的振幅。我们下面和加入噪声的图像比较。
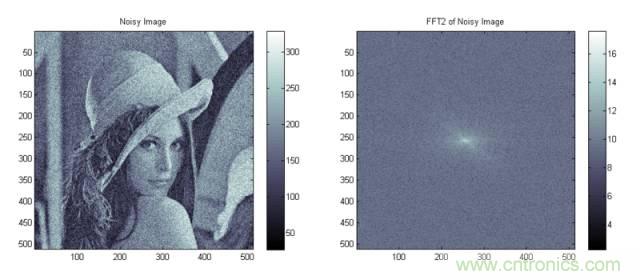
Lenna和她的频谱
现在,在图像中加入噪声。可以看到,原图像中各处增加了许多小“斑点”。这些斑点和原来的信号混合在一起。我们很难将一一指出这些噪音点。但另一方面,这些噪音又有一定的特征:这些噪音的空间尺度(即尺寸)很小。
这一对图像噪音的理解,可以从频谱中得到确认。从右图的频谱中可以看到,高频信号(非中心部分)明显增强。高频分量正对应空间尺度小的信号。可见,噪声在频谱中,集中在高频这一特定区域。这样,在与原图像混合在一起的噪声,在频谱上则和图像区分开。通过高频滤波技术,就可以过滤掉噪声。这也是图像降噪的一大方法。
(如果对图像处理有所了解,那么一定会知道Lenna的大名。她是一位阁楼(Playboy)女郎,但又是图像处理界的女神。你可以搜索"Lenna full image"来找到全图。Lenna现在是一名老太太了,她“见证”了图像处理的发展。)
5 总结
信号可以分解为不同频率的简谐波分量。这有助于我们更好的理解复杂的信号。傅立叶变换是信号处理(以及图像处理)的基础工具。通过傅里叶变换,我们可以获得信号的频谱。
频谱为我们提供了理解信号的另一个视角。在频率的世界里,我们可以发现很多原信号中一些可能被忽视的信息,比如降水的季节变化,比如增强的噪声。
免责声明:本文为转载文章,转载此文目的在于传递更多信息,版权归原作者所有。本文所用视频、图片、文字如涉及作品版权问题,请联系小编进行处理。
推荐阅读:
Digi-Key携手Option和GetWireless为其所有现场员工打造抗疫小徽章
高压断路器的操作结构有哪几种?和隔离开关有什么区别?
直流电能计量应用
瑞能半导体亮相2021慕尼黑上海电子展览会
伺服驱动器在电液伺服注塑机上的应用
