带通和带阻滤波器分析

品慧电子讯将并联和串联设计混合在一起的一种有趣的电路，是与输出负载串联的并联LC滤波器电路，下面我们将其称为（L // C）-R电路。下面的图1给出了这种架构的表示：

本文介绍利用并联L // C而引起的谐振现象，并利用该现象我们对电子中的滤波器模块进行设计。

带阻滤波器

将并联和串联设计混合在一起的一种有趣的电路，是与输出负载串联的并联LC滤波器电路，下面我们将其称为（L // C）-R电路。下面的图1给出了这种架构的表示：

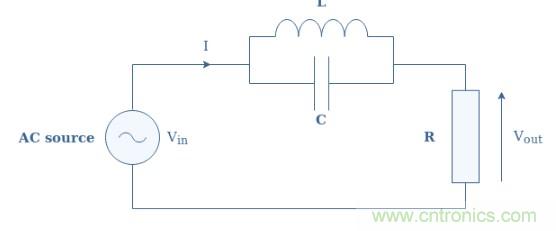
图1：（L // C）-R电路图

如果我们将Z L // C称为并联LC结构的阻抗，则可以写成V in = V out + Z L // C ×I。知道I = V out / R并通过用V out分解表达式，我们可以在几步之后写出（L // C）-R电路的传递函数：

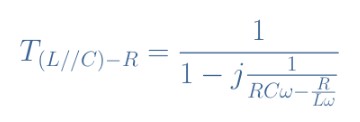
eq 2：（L // C）-R传递函数

我们假设L = 3 mH，C = 5 nF，R = 10kΩ和20kΩ，我们来分析该电路的传递函数，

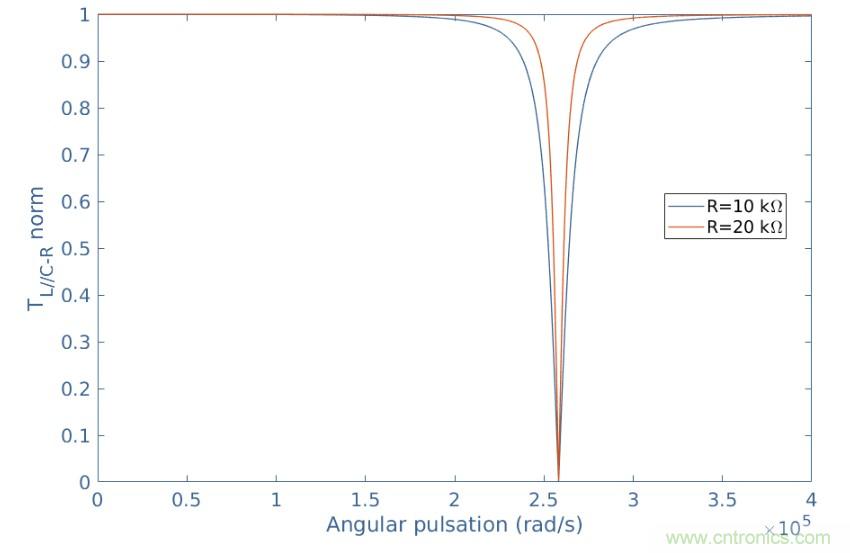
图2：（L // C）-R传递函数的图

图2陈述了这样的一个事实，即当电阻增加时，该带阻滤波器的带宽Δω变窄，这是因为Q 串联 =（1 / R）√（ L / C）=ω 0 /Δω。

实际上，该定义对并联电路无效，并联结构的公式变为Q 并联 = 1 / Q series =R√（C / L），这解释了先前确定的图1中的现象。

实际上，并联RLC电路的特征参数是串联RLC电路的倒数。

带通滤波器

一个有趣的概念称为对偶性，使我们能够从另一电路的知识中直接找到新电路的方式。基于这样的事实推论，可以将应用于电流或电压的方程式应用于特定结构。

让我们更清楚一点，再考虑一下上面详细介绍的带阻滤波器示例。我们将这种配置称为（L // C）-R，因为L//C电路与电阻R串联（-）。我们已经看到该电路充当该电压的带阻滤波器。

该电路的对偶电路是图3中所示的（L // R）// R电路：

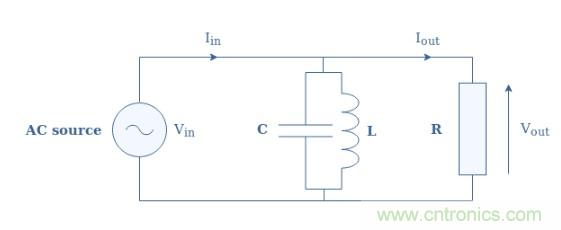
图3：图1的对偶结构

对偶性概念告诉我们，该对偶电路是带阻滤波器（即带通滤波器）的对偶。为了验证该假设，我们可以通过写成I in = I out + Y L // C ×V out来开始，这与上一节中显示的等式相同，但适用于电流，如对偶性概念所述。ÿ L// C是L // C的导纳和等于1 / Z L// C。

知道V out = R×I out并通过用I out分解表达式，得出：

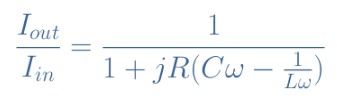
eq 3：（L // C）// R传递函数

我们可以看到，等式3与等式2非常相似，但是虚数项是相反的，这决定了了带通滤波器的行为。我们可以再次考虑相同的值L = 3 mH，C = 5 nF和R = 10kΩ和20kΩ，并绘制此传递函数，以得出本节的结论并确认带通滤波器：

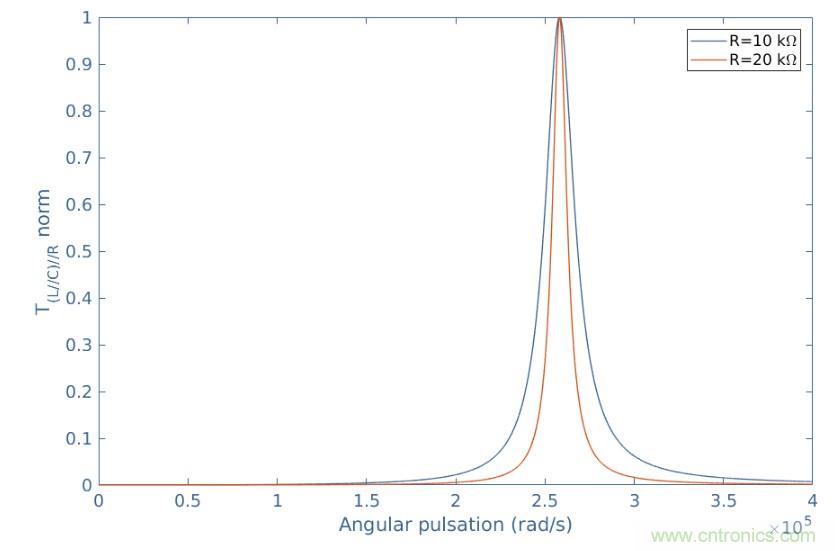
图4：（L // C）// R传递函数图

结论

并联RLC电路的行为与串联结构完全不同。这是由于L // C电路的能量相互交换的现象，称为共振。

这种现象是由于互连的电感器和电容器之间发生了相互放电/电荷。这样的电路的阻抗理论上趋于无穷大值在特定的脉动ω 0称为共振脉动（对于f或共振频率0）。在实际电路中，此阻抗会由于内部电阻行为而达到峰值。

推荐阅读：

贸泽将携手Silicon Labs举办低功耗蓝牙产品设计在线研讨会

安森美的汽车半导体方案使汽车更智能、安全、环保和节能

贸泽携手Bourns推出全新电子书，带你一起探索高性能电源转换元件

以中医“闻与切”的功夫，为工业安全把脉

艾迈斯的Jennifer Zhao当选为Questex“传感器创新周”的“年度女性”