二阶系统的运算放大器总输出噪声计算
品慧电子讯“指南MT-049”中分析了单极点系统的总输出噪声。下面图1所示的电路表示一个二阶系统,其中电容C1表示源电容、反相输入的杂散电容、运算放大器的输入电容或这些电容的任意组合。C1会导致噪声增益出现断点,C2则是为取得稳定性而必须添加的电容。
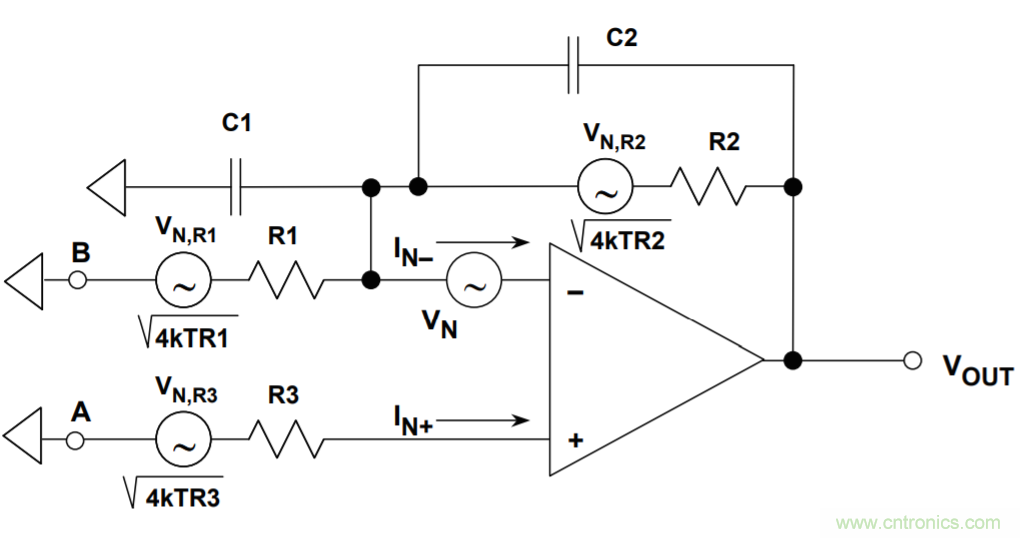
图1:带电抗元件的运算放大器噪声模型(二阶系统)
由于存在C1和C2,噪声增益是频率的函数,并在较高频率下有峰化现象(假定选择C2,使该二阶系统处于临界阻尼状况)。只要使R1×C1 = R2×C2,就可以实现平坦的噪声增益。
不过,对于电流电压转换器,R1通常为高阻抗,因此该方法不起作用。在这些情况下,要使信号带宽最大有点复杂,详见“指南MT-059”。
向输入端A施加直流信号(B接地)时,增益(即低频噪声增益)为1 + R2/R1。在较高频率下,从输入端A到输出端的增益变为1 + C1/C2(高频噪声增益)。
请注意,闭环带宽fcl是噪声增益与开环增益相交点的频率。向B施加直流信号(A接地)时,增益为–R2/R1,其中高频截止点由R2-C2决定。从B到输出端的带宽为1/2πR2C2。
同相输入端的电流噪声IN+流过R3会引起IN+R3的噪声电压,与运算放大器噪声电压VN和R3的约翰逊噪声√(4kTR3)一样,该噪声电压会被与频率相关的噪声增益放大。R1的约翰逊噪声会在1/2πR2C2带宽范围内放大–R2/R1,R2的约翰逊噪声则根本不会放大,而是在1/2 πR2C2带宽范围内直接连接到输出。反相输入端的电流噪声IN–仅会流过R2,进而在1/2πR2C2带宽范围内导致放大器输出端出现大小为IN–R2的电压。
如果我们考虑这六种噪声贡献,则会发现如果R1、R2和R3很小,那么电流噪声和约翰逊噪声的影响将降至最低,主要噪声将是运算放大器的电压噪声。随着我们增加电阻,约翰逊噪声和噪声电流产生的电压噪声将升高。
如果噪声电流很小,那么约翰逊噪声将取代电压噪声而成为主要的噪声贡献。不过,约翰逊噪声随着电阻平方根增加而升高,电流噪声电压则随着电阻增加而呈线性升高,因此最终随着电阻继续增加,噪声电流引起的电压将成为主要因素。
无论输入端是连接到节点A还是节点B(另一个则接地或连接到其它低阻抗电压源),上文分析到的这些噪声贡献都不受影响,这也是为何出现在运算放大器电压噪声VN上的同相增益(1 + Z2/Z1)会被称为“噪声增益”的原因所在。
要计算二阶运算放大器系统的总输出rms噪声,需要将这六个噪声电压分别乘以相应的增益,然后在相应的频率上进行积分,如图2所示(下图)。
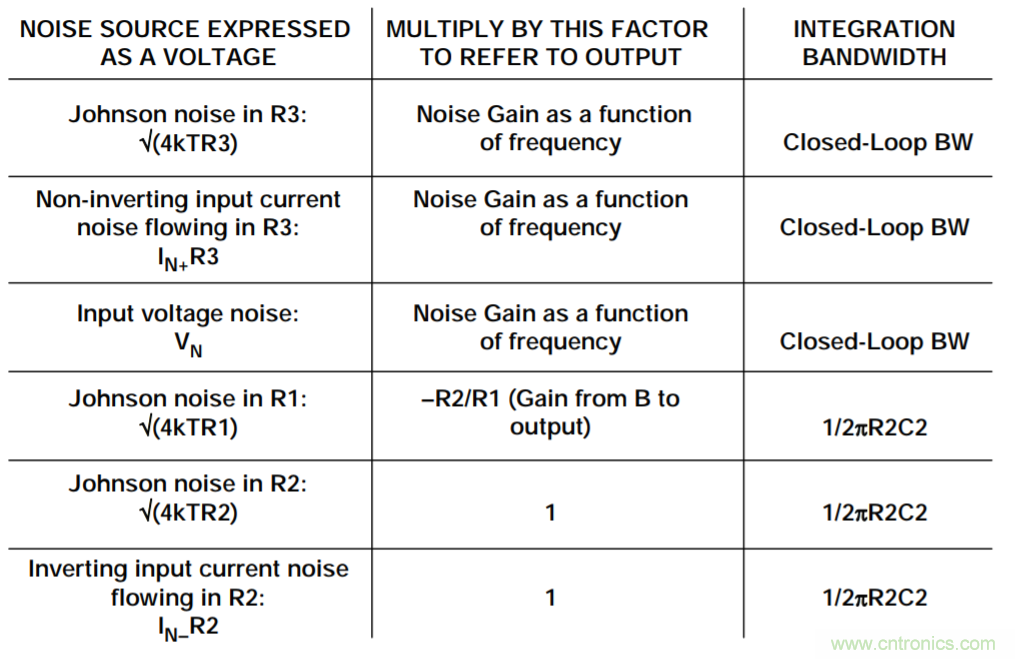
图2:二阶系统折合到输出端的噪声源
然后,所有输出贡献因素的和方根即代表总rms输出噪声。幸运的是,多数情况下,适当假设并识别主要噪声贡献因素,可以极大简化这个复杂繁琐的过程。
典型二阶系统的噪声增益如下面的图3所示。虽然两步内即可很容易地完成电压噪声积分,但请注意,由于存在峰化现象,因此输入电压噪声引起的输出噪声主要由噪声增益为1 + C1/C2的高频部分决定。这是二阶系统的典型响应类型。反相输入电流噪声、R1和R2引起的噪声仅在1/2πR2C2带宽上积分。
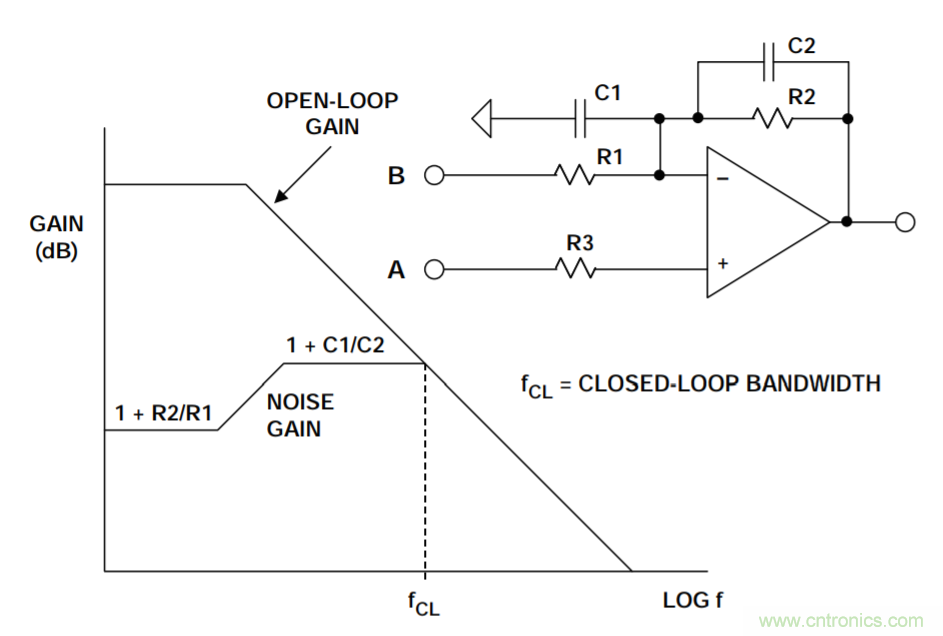
图3:典型二阶系统的噪声增益
参考文献
1. Hank Zumbahlen, Basic Linear Design, Analog Devices, 2006, ISBN: 0-915550-28-1. Also available as Linear Circuit Design Handbook, Elsevier-Newnes, 2008, ISBN-10: 0750687037, ISBN-13: 978-0750687034. Chapter 1.
2. Walter G. Jung, Op Amp Applications, Analog Devices, 2002, ISBN 0-916550-26-5, Also available as Op Amp Applications Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7844-5. Chapter 1.
推荐阅读:
使用片式NTC热敏电阻监控5G电子设备的温度
单极点系统的运算放大器总输出噪声计算
仪表放大器噪声
村田AMR传感器的特性及优势
无烦恼,高增益:构建具有纳伏级灵敏度的低噪声仪表放大器
