纯电感电路分析

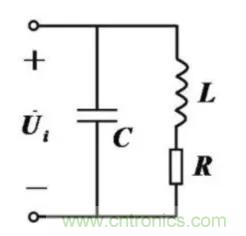
品慧电子讯由电阻小到可忽略的电感线圈组成的交流电路，可看作纯电感电路如下图，R=0时，就是纯电感电路。通常变压器、电动机等线圈或绕组可近似为纯电感性负载。

01电压与电流的相位关系

在电感两端加交流电压uL，电感线圈中将有电流iL流过，由电磁感应定律可知，线圈中产生的自感电动势eL起到阻碍这一交变电流的变化。由于忽略了线圈的电阻，根据基尔霍夫电压定律可知，uL与eL总是大小相等、方向相反，即

uL=-eL=-(-LΔiL/Δt)=LΔiL/Δt，

式子中ΔiL/Δt为电流变化率，如果电流变化率越大，则eL或uL的数值也越大；反之，电流变化率为0时，则eL或uL也为0。此外，电流变化率还有正负的区别，如果电流从小变到大，变化率为正，则uL为正值，eL为负值；反之，电流从大变到小，变化率为负，则uL为负值、eL为正值。

02电压与电流的大小关系

在纯电感电路中，对交流电流起阻碍作用的称为感抗，用符号XL表示，单位为Ω。

在交流电路中，感抗的大小与线圈的电感和电流的角频率乘积成正比，对于直流电路，可以认为角频率ω=0，则感抗XL=0。因此，交流电路中的感抗可表达为

XL=ωL=2πfL

纯电感电路中，电压、电流最大值或有效值与感抗之间的关系仍符合欧姆定律。即

ILm=ULm/XL或IL=UL/XL

03电路的功率

电感在交流电路中的瞬时功率pl=ul*iL，瞬时功率pL的波形也是正弦波，但其频率为电压频率的两倍。由于其正半周与负半周完全对称，所以电感电路所消耗的功率为零，即平均功率PL=0。

电路在第一和第三个T/4周期内，线圈从电源吸取功率，并把电能转换为磁场能力储存在线圈中。但在第二和第四个T/4周期内，线圈又把储存的磁场能量再转换成电能送回电源。因此，在一个周期T内，电感线圈中没有能量消耗，只是把电能与磁能进行周期性的交换。为了衡量电感和电源之间能量交换的规模，引进了无功功率的概念，其大小等于电感瞬时功率的峰值，称为电感无功功率，用符号QL来表示，单位为var(乏），表达式为

QL=ULmILm/2=ULIL=IXL