超详细:共模电感及滤波器的设计分析
品慧电子讯文中将详细地为大家分析如下看点:几个简单的实例测验与分析,共模电感“Z”字形符号解释,共模电感是否会饱和,共模和差模的概念,共模电感设计的几个经验以及一些重要的基本概念。
看点1 几个简单的实例测验与分析!
01 这是一个共模电感,如下测量,你觉得测得的电感量是多少?
可能有一部分会答错。
下面来说明一下
我们知道共模电感的绕法有两种,1 双线并绕,2 两组线圈分开绕。
1 双线并绕

2 两组线圈分开绕

正确的答案应该是10mH,下图所示。一楼所示的测量和如下测量一致。如仍有怀疑,可找个电感测量一下便知。
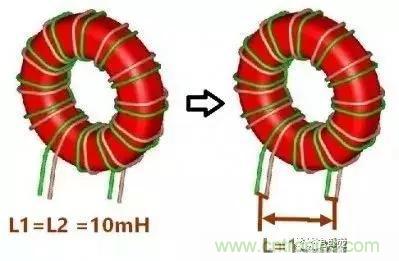
可以理解成两个电感并联,事实上就是两个电感并联,计算结果和测量结果是一样的。

两种绕法有何特点?
1 双线并绕
有较小的差模电感
有较高的耦合电容
有较小的漏感
2 两组线圈分开绕
有较小的耦合电容
有较高的漏感
因此要根据实际应用情况选择绕法。
02 再看看这样测量出来的电感量是多少?为什么?
有的人可能会回答0mH,有的人可能会回答20mH,有的人可能会回答10mH。
不过很遗憾都不是,正确的答案L=40mH。如下图,按右手法则已标上电流方向和磁通方向,从图中可以看出两个线圈的磁通的方向是相同的,也就是说磁通是增加的不是相互抵消。
根据磁环电感量计算公式

式中:N = 圈数, Ac = 截面积, 分母 Mpl = 磁路长度。
注意 N 有平方的,一组线圈的圈数是N, 则两组线圈的圈数是 2N,将2N代入到公式中分子有 4N², 也就是说电感量为 4 倍。本例则为 40 mH。
03 再看看这样测量得到的电感量应该是多少?这样测得的是什么电感量?
这个估计很多人都知道是0mH,没错,理想状态下就是 0mH。
实际共模电感总有漏感、或差模电感成份,因此按此连接测量得到的数值就是漏感或者叫差模电感。
共模电感中漏感和差模电感是一回事,可以称漏感也可称差模电感。一般做得好点的漏感在1-2%左右。
但有时候会特意将差模电感和共模电感做在一起,这时候的差模电感量就按实际需要做了。
看点2 共模电感“Z”字形符号是代表什么?
共模电感的这个符号应该很常见吧,但是符号中的的 “Z” 一样的符号该怎么读?估计很少有人知道。
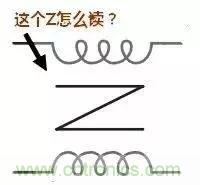
Z= Zorro (佐罗),很厉害的一个人物。共模电感也叫 Zorro 电感。英文中共模电感的叫法比较长 Common Mode Choke,或 Common Mode Inductor,也称 Zerro Inductor,有时简称为 Zerro。
举例: Fairchild 的 关于滤波器的文章中也是这么用的,如图:
看点3 共模电感会饱和吗?
共模电感会饱和吗?答案是非常难饱和,通常情况下无需担心饱和问题,为什么呢?我们先来看看差模电流流过共模电感的情况。如图,差模电流电流电感时其磁通是相互抵消的,也就是说,在磁路里基本没有磁通产生,差模电流流过时没有阻力,没有损耗,简单说,一个额定电流5A的共模电感流过100A的差模电流也不会饱和,当然前提是导线够粗。
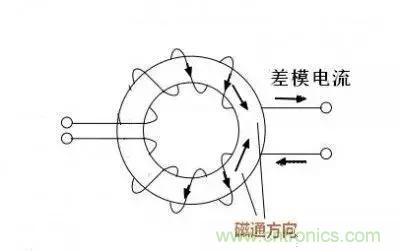
共模电流的情况相对复杂一点,百度了一下发觉都是抄来抄去,都是笼统的说阻抗增加,但并没有说明为何阻抗增加,基本没什么参考价值。
我们按如下方法分析一下:
假设一对共模电流流向如下图所示,两个滤波电感各自独立,没有磁通上的联系,这样能不能滤波共模电流呢?当然也能,相当于差模电感,各自为战,效果差一点。
于是我们讲两个电感合二为一,如图,这样会发生什么情况呢?
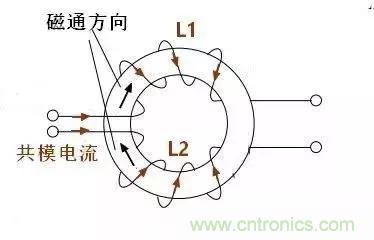
显然,流过L1的共模电流和流过L2的共模电流产生磁通相互叠加,总磁通增加。L1和L2除了自感以外还有互感,L1的电感量除了本身的电感外还要加上L2的互感,反之L2也一样。
这样情况又要分几种:
1)L1的磁通会使L2产生互感电动势,互感电动势的方向总是要阻碍磁通的增加,于是在L2中产生和共模电流方向相反的电流,L2的共模电流被抵消,反之,L1对L2的互感电流也是与L1的共模电流方向相反,也就是说L1的共模电流被抵消。如下图所示,L2中的互感电流与L2的共模电流方向相反的:
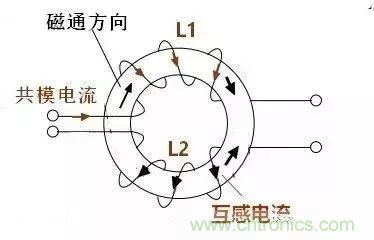
2)电感量计算,如图:
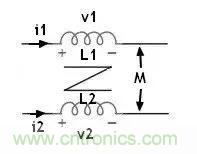
根据自感公式:
则L1的有效电感为:
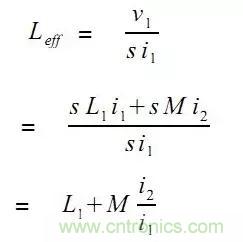
设:
于是有:
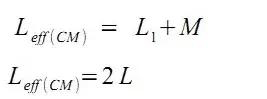
即共模电感量为绕组的两倍。
对于差模电流有:
于是,差模电感
即:
也就是说差模电感量为0。
看点4 共模和差模的概念
共模和差模的概念:这个很好理解,看一下图便知。
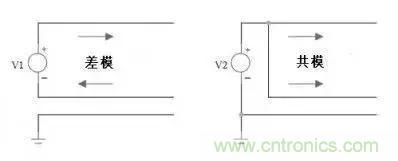
共模干扰来之何处?共模干扰的频率如何?1MHz以上还是5MHz以上?如图:
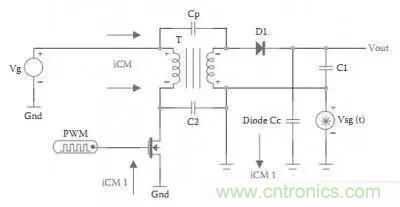
共模干扰由MOS管的高di/dt引起,经过变压器间的电容Cp或杂散电容C2传到副边,以Cp为主,C2基本可忽略。我们知道Cp很小,因此能传到副边的干扰频率一定很高,低频干扰信号过不去,因此EMI测试中的高频部分基本就是共模干扰。究竟多少MHz与变压器的结构有很大的关系,层间电容大了则可能1MHz的共模能过去,层间电容小了,则只能是更高的频率能过去,比如5MHz以上。
由此可见,变压器的绕制对EMI有不可忽略的作用,并且需要在漏感和绕组电容中折中考虑,漏感小了则初次级的电容一定大了,初次级的电容小了则漏感大了,初次级电容小则有利于抑制共模干扰,但漏感大了会在给原边的MOS管带来压力。
如何既能减小原付边电容又保持漏感小呢,目前看来=只有一个办法,在原付边件加屏蔽。简单说,在原边和付边之间一圈不到的铜箔,铜箔不可绕满,不可重叠,留1mm左后的空隙。实测效果不错的,但变压器绕制就复杂了。
我们来认识一种新的电容,其实也不是新的只不过估计很少有人知道,很少有人用。
如图,称为 Feedthrough 电容,专门用于EMI抑制电路,其抑制高频干扰效果相当好。

其内部等效结构如图
其在电路中的符号为:
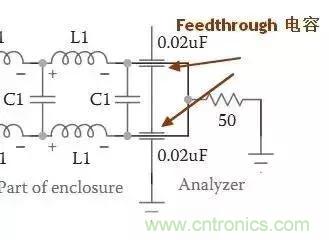
其特点为,低ESR,低ESL,高谐振频率,因此专用于EMI抑制。
其参数等详细资料可网上搜索厂家的说明书。
以下的图应足够能说说明这个电容。
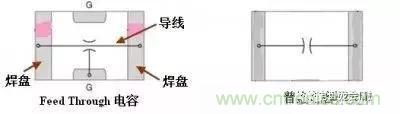
从上面的做图可以看出这种电容的内部其实是导线(实际有电感),导线外面通过做成电容形式,并把电容一端接地,因此低频或直流信号完全不受阻,但高频则会通过电容接地。由于该电容没有引脚,因此ESL(等效串联电感)很小,这个至关重要。
有必要说明一下为什么电容的谐振频率要高。
如图,所有电容的ESR和阻抗曲线都有相似形状,只是ESR或谐振点的位置不一样,图中谐振点左面电容呈容性,即具有电容的特性。但是工作频率高了以后,电容的容性越来越小,过了谐振点后,电容的容性便消失,于是电容变成了电感。可想而知,本来在电路里放了一个电容,结果变成了电感,那是什么后果?
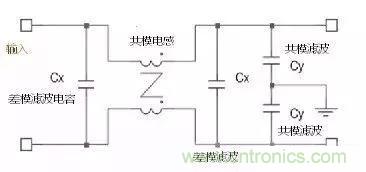
认识一下典型的滤波电路,如图所示:
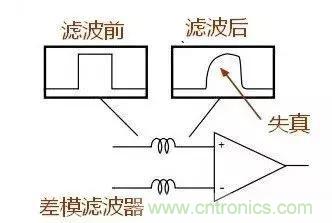
共模滤波器和差模滤波器对差模信号滤波效果对比,差模滤波器在滤出叠加在信号上的噪声后导致波形失真。
但使用共模滤波器滤出信号上的噪声后波形没有失真。
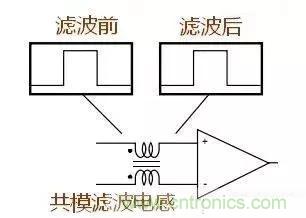
因此,对于数字信号如有噪声需滤除采用共模滤波器比较合适。
说滤波器就不能不说滤波器的阶数,谈到滤波器我们可能会听到或看到滤波器的阶数,那么什么是滤波器的阶数呢?我们看以下最简单的RC滤波器,那是几阶?
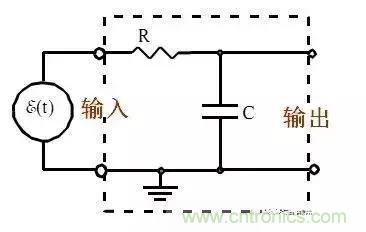
答案是:一阶,英文叫 First Order
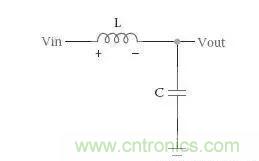
那这种呢?
还有这种滤波器是几阶的呢?
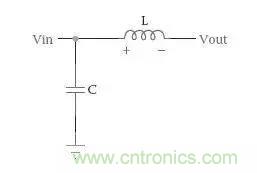
答案都是二阶,英文叫 Second Order
这样说应该明白什么是滤波器的阶数了吧? 简单讲,有多少个储能元件就是几阶,RC滤波器只有一个电容则是一阶,LC滤波器有两个储能元件则是二阶,与前后关系无关。
如下最常见的PI滤波器就是三阶的了
那么一阶、二阶、三阶滤波器性能上有何区别?
可以滤什么频段是电感电容取值问题,但不同阶数的滤波器还有更重要的特性,就是衰减信号的斜率问题。
我们先弄清十倍频这个概念:
十倍频,这个应该不难理解,从数轴上看,十倍频就是频率增加10倍,比如 2 到 20Hz 就是一个十倍频,那么 50 到 5000Hz 是几个十倍频呢?
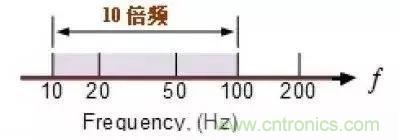
我们以一阶和二阶滤波器的衰减曲线为例,见图
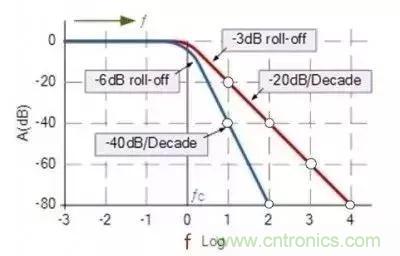
图中横坐标是频率,用对数表示,纵坐标表示增益,单位为dB,注意图中的圆点处,右面一条是一阶滤波器的衰减曲线,圆点从1 到 2 频率增加了十倍,从纵坐标中可以看到增益下降了20dB,通常称为10倍频程衰减20dB,左面一条曲线是二阶滤波器,不难看出10倍频程衰减40dB。
由此可知,滤波器每增加一阶,十倍频程衰减增加20dB,如下图所示。
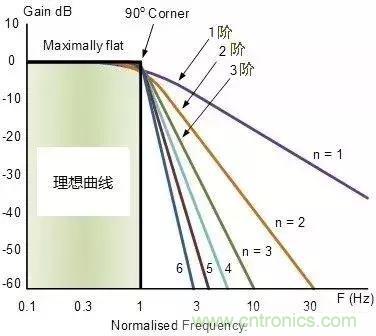
看点5 几个疑问
小测验:两个电感,圈数一样,直径一样,但绕制的长度不一样,哪个电感量大?
小测验:如图,两个电感圈数一样,线圈高度一样,直径不一样,哪个线圈电感量大?

线圈不同直径 或 不同长度的形成的电感量参考以下截图,式中 A 是线圈面积,l 是线圈高度,(注意不是磁芯的长度),按公式可以看出,面积越大电感量越大,线圈高度越小电感量越大。
需要注意的是,这个公式仅仅表示表示几个量的相互关系,不能算出准确的电感量的。
如图,一棒形电感(或工字形电感),在一端截去一部分磁芯,其电感量是增加了还是减小了?为什么?

问题:你买了一批工字磁芯(或磁棒)要加工成1mH的电感,需要绕多少圈如何计算?
工字磁芯或磁棒做电感算是算不准的,通常的做法就是试绕一定的圈数(比如绕一层)然后测量一下电感量,算出每圈的电感量然后再按此算出总的圈数,由于内圈和外圈的直径不一样每圈电感量也就不一样,因此绕好后还得测量进行修正,有时厂家会给出有效磁导率,可参考,线圈在磁棒上的位置不一样(靠近磁棒中心还是靠近两端),疏密程度不一样电感量均不一样。
棒形电感有气隙吗?当然也有,棒形电感的气隙就是端点到端点的距离,如图所示棒形电感的气隙是非常大的。
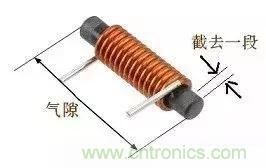
棒形电感的气隙性质与磁环的气隙性质有明显不同,如图,磁环开气隙后其等效磁导率与没有气隙的磁环的磁导率相比小很多,气隙越大等效磁导率越小,反过来说气隙越小等效磁导率越大。

那么问题来了,磁棒截去一段后端与端的距离变短了,也就是气隙变小了,但实际电感量也变小了,一种解释是等效磁导率变小了,如图所示。
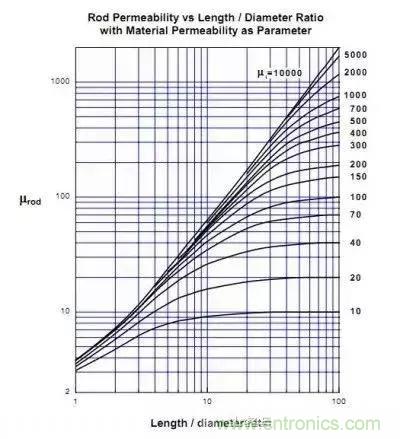
这个图是被各种资料千万遍引用的,属于最经典的。这个曲线无非是实测以后得出的统计数据,并未道出问题的实质,而我们希望知道为何总得磁路短了电感量反而变小。
图中横坐标是磁棒的长度与直径之比,随长度变短气隙变小等效磁导率也变小,这好像不合理,我们看磁环的电感计算公式:
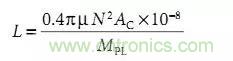
MPL表示磁路。
我们知道磁环的气隙变小电感量会变大有效磁导率也变大。因此磁棒的气隙变短了其等效磁导率应该变大并且电感量也应该变大才对啊,但事实相反,一定是哪里有问题了。
原因其实很简单。真正的磁力线的密度其实是很高的,不像我们平时那么画几条意思意思的几条。
可能这样:
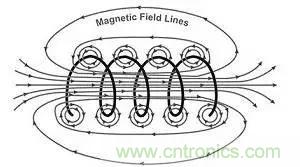
真正的原因是因为磁芯外部的磁场会在磁芯上产生感生电流,此电流方向与线圈电流反向相反,感生电流同样会产生磁场,该磁场的方向与磁芯内原来的磁场方向相反,彼此互相抵消一部分,当磁棒被截短后,外部磁场增强,磁芯上的感应电流加大从而反向磁场增强,于是削弱了线圈产生的磁场,最终导致电感量减小。
看点6 共模电感设计的几个经验
共模电感的设计:共模电感设计很简单,掌握以下步骤即可:
1) 尽可能选用磁导率高的磁芯以获得最大的阻抗(对付30MHz以下的干扰MnZn,30MHz- 1 GHz用NiZn),
2) 选择适合饱和磁通的磁芯,确保最大共模电流时磁芯不会饱和,(通常共模饱和电流只有3-5mA)
3) 选择功率损耗小的磁芯
4) 在选定磁芯尺寸下绕尽可能多的圈数
5) 选用尺寸小的磁芯
6) 线间距尽可能大以减小杂散电容(避免高频信号通过杂散电容耦合过去)
7) 由于绕线有电阻会发热因此需要合适的线径
电感的能量储存在哪里?
这是个颇有争议性的话题,我们通过以下实例来研究一下:
如图是一个电源、一个开关、一个电阻和一个电感串联在一起。初始状态开关打开,电路中没有电流。
现在我们将开关合上,会发生什么情况?这可以从两个方面看:
1)电路理论:当一个电感中有变化的电流流过时电感两端会产生感生电动势(V = L di/dt),这样电感中不但有电流还有电压则其功率为 P= IV,既然有功率毫无疑问变化的电流带来了能量。
2)物理学: 变化的磁场产生电场,而这个电场力则拼命将电子推回去,在推的过程中不断获取电子的能量,而电源则不断给电子增加动能以通过电感,这样电感电流不断加大,电子的动能越来越强于是电场也越来越强。
随着电流最后达到最大值1A,电感中的磁场不再变化,于是电感两端电压为0,(di = 0,V = L*di/dt = 0),于是电场强度也变为零(变化的磁场才会产生电场)。
随后我们将电源电压突然调为0V,结果会怎样?
随着电压调到0,电子从电阻上流过能量逐渐在电阻上消耗掉,电流的变化再次建立起变化的磁场,而变化的磁场再次建立起电场,而此时的电场力给予电子能量并推动电子加速流出,随着能量的耗尽,电流最后为零,磁场也逐渐消失。
如果在电流流动过程中我们突然打开开关,使电路呈开路状态会发生什么情况?
电子正在有序的向前流动,此时开关突然断开,于是所有电子不得不紧急停止,电流于是突然就变为零了,于是磁场瞬间崩溃,磁场崩溃过程中在电感两端感应出极高的电压(V = L*di/dt,dt趋于0),同时瞬间变化的磁场产生极强的电场,这强大的电场推动所有电子往前跑。不难想象这时在开关断开处的电子的心里那个急啊:别挤别挤,再挤掉下去了,然而后面的电子不知道啊,在电场力的作用下如潮水般涌来,呵呵.
突然想起一句广告词叫做 “真的停不下来”。于是挤成一团的电子在强大的电场力下不得不一起冲出导线跑到空气中,其电压之高足以击穿空气(V = L*di/dt,dt趋于0),于是通过空气向开关的另一端放电产生火花释放能量或者看谁离得近不顺眼的就向谁放电以释放能量。
如图是螺旋线圈中磁场和电场的关系示意图,电场方向是沿线圈圆周的切线方向,而磁场在图中是垂直穿过。
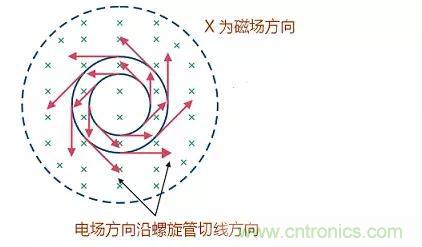
看点7 一些重要的基本概念
1 电磁场:电场和磁场总是联系在一起的,电场和磁场的混合就是电磁场,英文也专门创建了这么一个单词(Electromagnetic Field 电磁场),以下图为例,
图中是一小段PCB铜箔的截面,大小不断变化的电流面向正面流进或流出,注意是变化的电流,因此产生了变化的磁场,由此也感应出电场,注意磁场的方向是环绕铜箔的,而电场是从铜箔指向参考面,参考面为地平面。磁场和电场这个方向特性要记住,在进行PCB布线线时为减小对其他电路的干扰可适当注意与磁场方向其他导线或电路成某种角度。
2分贝(Decibel):分贝是基于对数的单位,EMI测量中都用分贝作为基本单位的,因此对分贝需要有所了解。
分贝的基本定义:10log10[测得的功率/单位功率]
比如,测得5000mW,则10 log10[5000mW/1mW] = 37dBmW = 37dBm
注意通常 dBmW 是写成 dBm 的,其W是省略不写的。
如果用dBW作为单位,则37dBm = 7dBW,注意换算关系。
而实际EMC测量中都是测量的电压或电流,通常是微伏或微安,最常见的就是 dBuV,这时候的坐标就不是10log了,而是20log,需注意。
这张表需要大致知道了解一点的
特别是表中三个框中的关系要知道,比如信号强度增加一倍则功率增加3dB,电压或电流增加了6dB。仔细体会一下,信号增加10倍功率增加多少倍,电压或电流增加多少倍。
3 电流的返回路径,这是非常重要的概念:
3.1,低频电流按最小电阻路径返回,高频信号从最小阻抗路径返回,这是因为每一段导线都包含电感和电容。通常频率以50KHz为分界线。
3.2,差模电流返回一定有路径,你把路径切断差模电流就没有了。
3.3,共模电流你一定要给它路径,你不给路径它就乱窜,造成严重的EMI问题。好似流氓,你给他一条生路他就比较太平,你不给他生路他就搅天下不太平。这也是为什么变压器原边和附件加Y电容给共模电流提供一条返回路径。共模电流都是uA级或mA级,电流虽不大,但破坏力惊人。
3.4,差模电流返回路径的包围的面积一定要小,面经越大产生干扰信号越大,吸收外界的干扰也大。如图所示
4 时域和频域
时域是真实存在域,我们用示波器观察到的波形就是典型的时域,所谓眼见为实。
频域是一种数学构造,是假设用某种波形来构建不同的波形,通常是用正弦波,这不是我们这里要讨论的问题。
而EMC测量都是采用频域的方式,例如用频谱仪或EMI接收器等。为什么要用频域的方式测量EMC呢?我们知道,方波可有很多个(或无数个)正弦波构成,如下图:
但每个正弦波的频率额幅值是多少呢?用时域的方式测量很难,于是借助于频谱仪,我们可测得每个波形的幅值及频率,而这些频率正是干扰频率,称为谐波,其幅值反映了干扰的强度。如图所示:
再次强调:谐波的频率是基波的整数倍。比如100KHz的矩形波,其谐波为300KHz、500KHz等。
5 三种无源器件的高频等效模型
5.1,电阻的高频等效模型
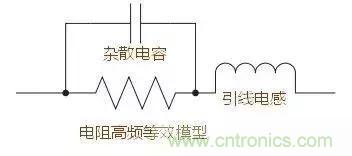
5.2电容的高频等效模型
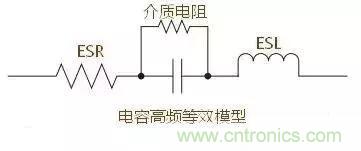
5.3,电感的高频等效模型
6 近场和远场
顾名思义,近场就是靠近电磁场,远场就是远离电磁场。
对PCB来说,电流回路一般以磁场为主,而大面积的金属面(例如铺铜、散热器表面)以电场为主,或者说大电流的路径上以磁场干扰为主而高压部分则以电场干扰为主,或者说低阻抗路径以磁场为主而高阻抗路径以电场为主。因此有时大面积铺铜散热需要考虑该散热面上是否有高压,有高压则会产生干扰电场。而大电流导线最好离敏感电路离得远一点。(恒定电流不会产生干扰磁场,有干扰一定是有变化的电流引起)。至于电磁场强度则通常借助于近场探头来进行测量。
7 电感的品质因素 Q
Q 是 Quality的第一个字母,电感的品质因素定义为:
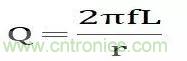
由上式可见品质因素是与频率有关的量,在 r 不变的情况下,频率越高则品质因素越高,然后通常我们不太使用Q这个量,而通常更关心的是Rdc,即电感的直流电阻,与电容类似,我们通常关心的是等效串联电阻 ESR,而不是tgδ。电感线圈的直流电阻与电容的 ESR 一样可通过电桥测得。
8如何数电感或变压器的圈数?
问题看似很简单,试试看如下线圈是几圈?
9 近场探头及探测原理
探测原理并不复杂,示意图一看就明白

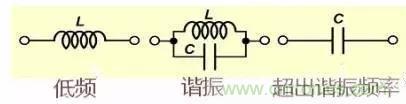
10 电感线圈的三种等效电路(忽略等效电阻)
电感线圈在低频、谐振及工作频率高于谐振频率时会呈现不同的特性,特别是当工作频率超过谐振频率是电感不再是电感而变成的电容。图中的电容是线圈的匝间电容。
11 为什么MOS管脚上套个磁珠能起到抑制噪声的作用?
虽然大家一直在这么用,但估计很少人会问为什么?我们先看看下面这张图,这个磁环中间穿了根导线,你说这导线是饶了几圈?

可能有人会说没有绕啊,哪来的圈数?
事实上,导线穿过磁环就是饶了一圈,为什么呢?道理其实很简单,这根导线如果没有接入电路那确实是没有绕,只要一接入电路就是一圈,它总要和电路构成回路,比如我们用电桥测量,如图,这根导线就和电桥构成了回路,也就是形成了一圈。

MOS管脚上套个磁环后,MOS管的脚总是和外电路构成闭合回路,也就相当于MOS管脚在磁环上饶了一圈。由此可见,磁环的磁导率越高滤波效果越好。
12 插入损耗
如何评价一个滤波器的性能?通常采用插入损耗来评价。如图示意图表示信号 V1 --> V20,V20 表示没有滤波器时的输出。
为了对V1进行滤波于是插入了一个滤波器,将V1信号损耗在滤波器上,于是就有了这个名词叫插入损耗。V2 表示插入滤波器后的输出。

插入滤波后,会有什么结果?V2 一定小于 V20,也就是说插入滤波器后输出变小了,为何输出变小?一部分变成热量、一部分被滤波器挡住返回了,如图:
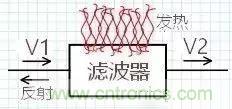
插入损耗按下式计算:
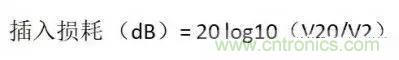
式中:V20为未加滤波器,V2 为加了滤波器。
13 传导测试方法,
下图是实验室传导测试的标准方法,建议各位花一分钟时间看一下,了解实验室是如何测试传导干扰的,终身受用。
14 输入端L C滤波器设计注意事项:
输入端LC滤波器的一般形式如下:
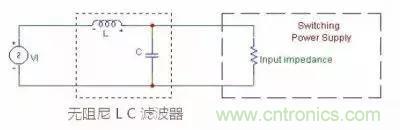
有于滤波电路中有两个储能原件因此是两阶滤波器,这滤波器有个很大的问题,由于无阻尼,因此当干扰信号的频率达到滤波器的截止频率时(Cut off),干扰信号不但没有被抑制反而被放大了,如图所示:
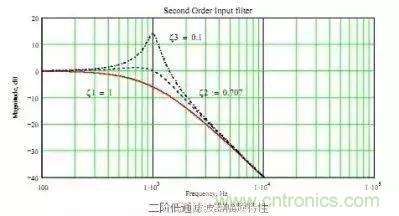
从图中可以看到,当阻尼系数为0.1时,干扰频率在 f0 处明显被放大。阻尼为0.1时尚且被放大很多,没有阻尼那更是不得了。
f0 = 1/2Π√LC, 为谐振频率。
这可是事与愿违啊,我们本想抑制干扰但由于设计不当干扰非但没有被抑制反而被放大了,这可不是我们所希望的。
当然,阻尼为零的情况是不存在,电感电容总有内阻,因此总有些阻尼作用的,但这远远不够,而且不可控。通常采用以下几种方法解决:
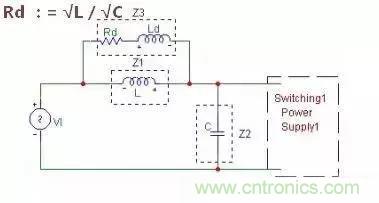
1)并联阻尼法,如图
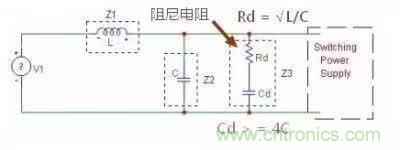
加阻尼后的幅频特性
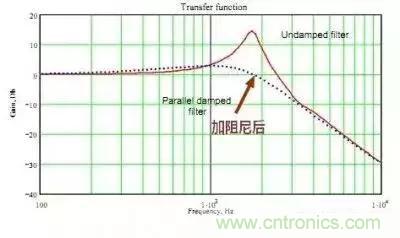
可以看出,截止频率处的尖峰被压平,也就是说不再使得噪声被放大。其中电容 Cd 对阻尼不起作用,只是为了隔离输入电压以避免电阻产生
方法2:串联阻尼法
如图:在电感上并联一个电阻与电感串联的电路,这称为串联阻尼法,效果与并联阻尼相同,不足之处是由于在原电感上并联电阻电感后对高频干扰信号的衰减差一点,这是显而易见的。事实上大部分的实际应用中Ld 都被省略了,仅仅在电感上并联一个电阻,这个电阻称为阻尼电阻,目的与前述一样防止在截止频率处把干扰信号放大,实际使用中阻尼效果还是不错的。
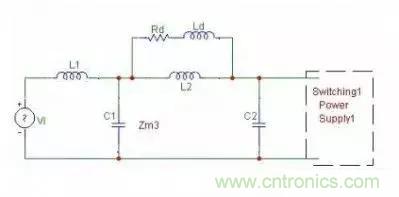
方法3:串并联法:
这种方法用的人估计不多,了解一下即可,如图:
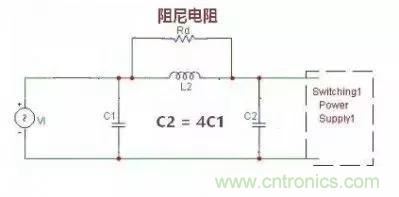
方法4,Π 滤波器
这是用的最多的一种,如图,通常都仅仅在电感上并联一个阻尼电阻,这个阻尼电阻不可少,曾经看到有些贴问这个电阻干什么用,有各种说法,但很少有说对的,请记住这个是阻尼电阻,为了消除干扰信号在滤波器的截止频率处产生尖峰,达到243楼的的幅频特性的加阻尼后的效果。有人说前面一个C1电容可以省去,这个说法不对的,我们前面已讲过,每加一个储能元件 L 或 C,滤波器的阶数并升高一阶,对信号的衰减可以增加20dB/十倍频程,pi 滤波器是三级滤波器,把C1拿掉后变成了二阶,滤波效果会打折扣。
一个实例:
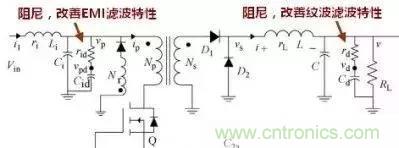
这是一个正激电源,请特别注意,输入LC的EMI滤波器和输出的纹波滤波器都有一个电容串联电阻的阻尼电路,阻尼作用前面已多次提及。特别注意输出端的阻尼电路,曾经见过帖子问为何在电解电容上串联一个电阻,但似乎都没有人知道为什么,请记住这是为了改善纹波性能加上的阻尼电路,有了这个阻尼电路课大大改善纹波性能。道理同EMI滤波器的阻尼相同。
15 共模电流会经过负载吗?
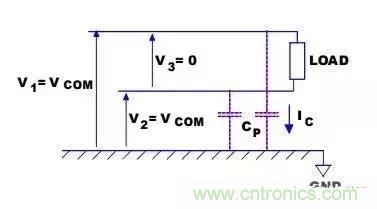
答案是否定的,共模噪声电流对用户的负载其实没什么影响,因为共模电流并不流过负载,如图所示,由于共模电压V3 = 0, 因此负载上并没有共模电流流过,共模干扰信号只会以各种方式到 “地”。
16 滤波器的Q值
Q = Quality,Q 是取 Quality 的第一个字母,是一个无量纲的值,滤波器的 Q 值是一个相当重要的值,理解及取适当的 Q 值 相当重要。
滤波器的 Q 值大小表明了能量在滤波器上损耗的大小,并且对滤波器的带宽有很大的影响。Q 值越大能量损耗越小,这与电感的 Q 值一样道理一样,Q 值越大则能量损耗越小于是振荡衰减越慢,这与反激原边RCD吸收电路一样,能量的损耗主要依赖电阻。
有些电路我们需要高 Q 值,比如振荡器,Q 值越高越容易起振,比如收音机机调谐回路,Q 值越高选台时越不容易串台,这主要是 Q 值高时-3dB带宽变狭的缘故。如下图所示:
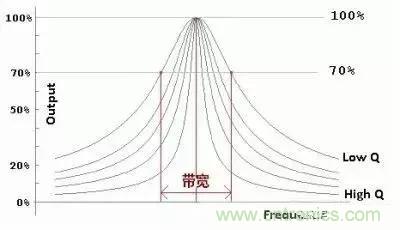
Q 值定义:
Q 值定义如下:
分子为存在与滤波上的能量
分母为每周期消耗的能量
或

意义如下:
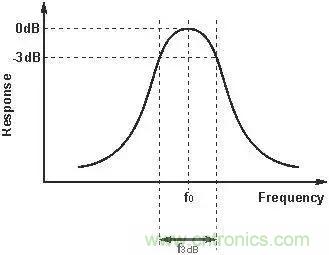
Q 值得意义:
虽然是老生常谈,但还是要再提一下:
Q< 1/2,,过阻尼。系统损耗很大,施加阶跃脉冲后,系统没有过冲并很快稳定下来。
Q > 1/2,欠阻尼。系统损耗很小,如果Q 率大于1/2,在阶跃脉冲作用下,系统会有1次 到 2次的振荡,随 Q 值得增大,系统的振荡次数会越来越多,理论上如果 Q 值无穷大,则系统将永远在振荡。
Q = 1/2,临界阻尼。系统没有过冲,在阶跃脉冲作用下,会很快趋于稳定。
关键的问题是 Q 取多大为好?
答案是 Q = 5-10
答案是引用以下资料(在文章的结尾),文章不错,对于设计LC滤波器及pi滤波器有参考价值,值得一读。LC Resonant Circuits.
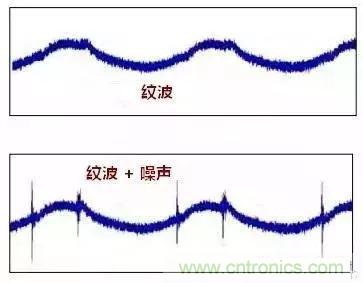
17 分清纹波和噪声
常有人描述问题时把纹波和噪声混为一谈。纹波是低频的,噪声是叠加在纹波的干扰信号。如图: