模拟集成电路之频率响应分析零极点
零极点的理解是模拟电路最关键的基础之一,信号与系统都会讲自然响应,自然响应就是偏微分方程的通解部分,而受迫响应则是偏微分方程的特解。本文将详解零极点与频率响应之间的关系。
我们从频率域来分析零极点的影响。从频率域上,零点和极点会决定系统的频率响应。我们令系统传输函数H(s)中s(=σ+jω) 的实部σ=0而虚部ω仍然是变量,就得到了频率响应函数H(jω)。频率响应函数代表系统在恒包络正弦小信号输入时,输出正弦信号相对输入正弦信号的幅度和相位变化。频率响应函数可以表示为:
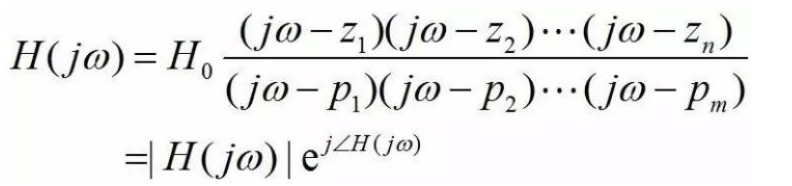
频率响应H(jω)是复数。其幅度|H(jω)|代表当正弦信号频率为ω时,输出正弦信号幅度相对输入正弦信号幅度的比值(即系统的增益),而其相位∠H(jω)则代表输出正弦信号相对输入正弦信号的相位变化。根据高中数学,频率响应的幅度和相位可以表示为各个零点/极点的贡献:
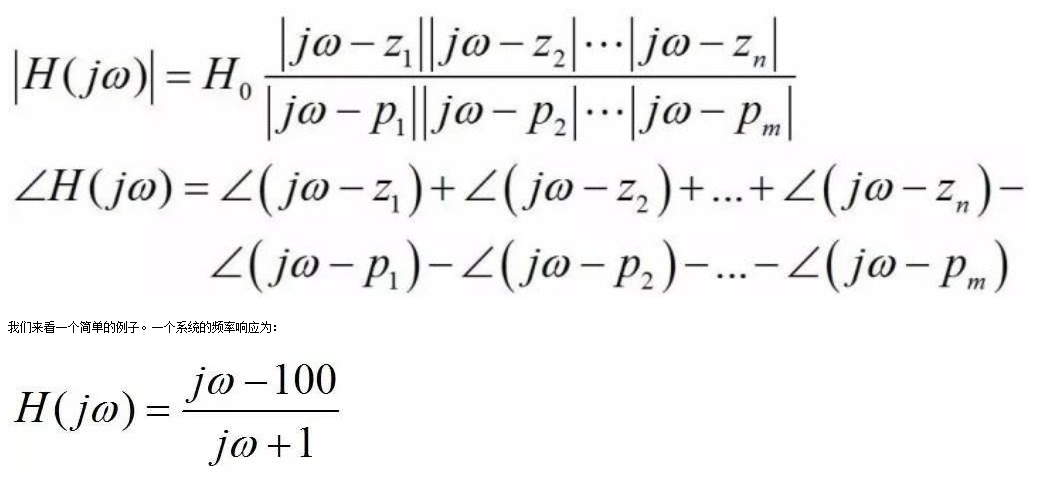
它有一个极点(实部σ=-1,虚部ω=0,其模为1)和一个零点(实部σ=100,虚部ω=0,其模为100)。由于极点的实部小于0,该系统是稳定的。当ω=0的时候[即DC(直流)响应],分母的模为1,相位为0,分子的模为100,相位为π,因此频率响应的幅度为100,相位为π。我们接下来增加一点点ω,让它等于0.001。这个时候ω远远小于极点的模,因此频率响应分母的值和DC时没有显著区别(1+j0.001≈1)。ω也远远小于零点的模,因此频率响应分子的值也和DC时基本相同。所以当ω的值远远小于某个极点/零点的模的时候,该极点/零点的效应可以忽略不计。这也是在实际电路设计中很多频率远高于电路工作频率的极点/零点在分析的时候可以忽略的原因。当ω增加至1时,分母变为(j1+1),此时分母的幅度由DC时的1变为√2,相位则由0变为π/4。由于ω仍然远小于零点(1《《100),分子较DC相比仍然没有变化。频率ω=1时对极点是一个转折点:随着ω继续增长,该极点的效应渐渐变得显著。当ω=10的时候,ω已经远远大于极点的模,因此频率响应的分母可以近似为jω,相位为π/2。此后随着ω继续增长,分母的模随之变大,因此在零点发挥作用前,频率响应的幅度会随着频率增大以20dB/dec的速度减小。另一方面,当ω增大到远大于零点的模(》》100)时,频率响应的分子可以近似为jω,因此分子的相位为π/2,且分子的模随着频率增长以20dB/dec的速度增长。此时分子和分母的模都以20dB/dec增长,因此互相抵消,频率响应的幅度不再变化,而相位则由DC时的π变为0。
H(jω)的幅度和相位
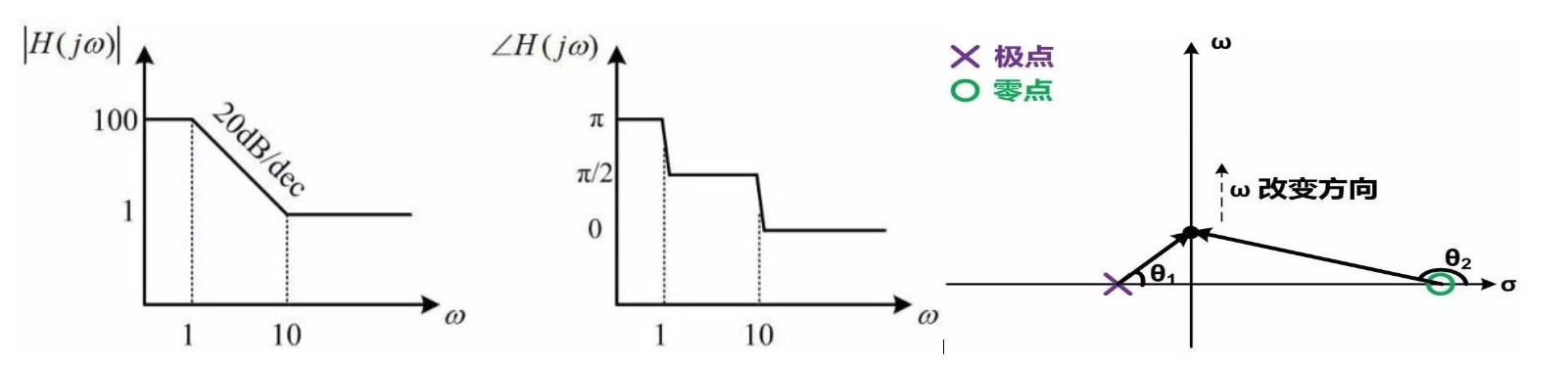
零点和极点对频率响应的效果也可以由s平面零极点图解释。上面例子的零极点图如下:
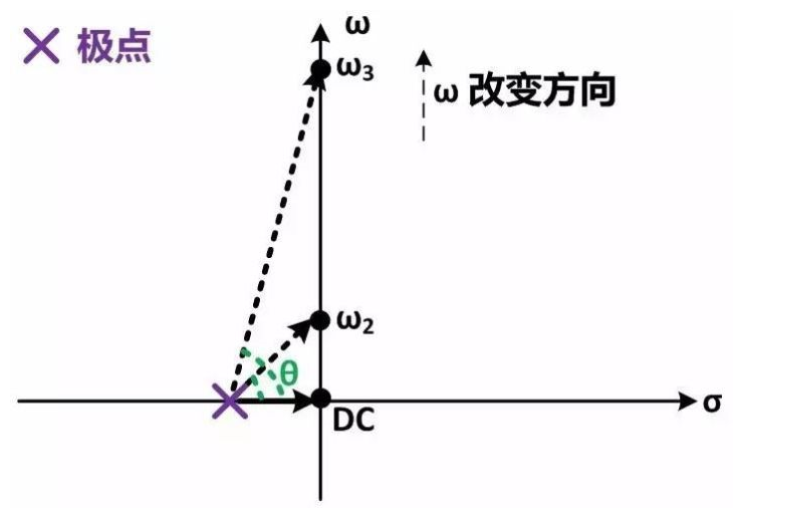
开始ω1=0 (即DC响应),极点向量的相位为0。之后随着ω增加,极点向量的长度逐渐增长,相位贡献θ也逐渐变大。当ω等于极点的模的时候(ω2),根据初中数学极点向量的长度变为DC时的√2倍,而相位角θ为π/4。之后随着ω继续增长到远大于极点的模的时候,极点向量渐渐变得和ω轴平行,此时极点向量的长度近似等于ω,而相位角θ也渐渐逼近π/2。对于零点也可以做类似的分析。这样图解分析与之前分析的结果相同,但是更直观。
