变压器的轻微匝间故障保护分析
变压器的轻微匝间故障保护分析
摘要 首先对一次110 kV/10 kV，31 500 kV.A变压器的轻微匝间故障进行了分析，继而导出对变压器轻微匝间短路的实用计算方法。最后根据轻微故障的特点提出对变压器比率差动继电器通用特性选择的建议，供同仁参考。
Transformer Protection for Low Percentage Interturn Faults
Zhu Shengshi (Nanjing Automation Research Institute，210003，Nanjing，China)
Abstract The analysis of an interturn fault about one percentage turns is introduced and a calculating formula for estimating the interturn fault current of the transformer is derived.According to the calculation result and features of low percentage interturn fault,the general characteristic selection for percentage differential relay of transformer is suggested. Keywords Transformer,Interturn faults,differential protection
1 变压器的轻微匝间短路故障实例及分析 1997年5月6日开封滨河变一台110 kV/10 kV，31 500 kV*A变压器发生事故，变压器差动保护正确动作跳闸，瓦斯保护未动作。 事故后对变压器进行各种外部试验都未能发现故障。内部检查为高压侧A相匝间短路，被短路的匝数约占全部绕组的1%。这次事故是典型的轻微匝间故障，对此有深入分析研究的必要。 图1是该事故的故障录波图，其显示高压侧三相电压和低压侧电流都没有明显的变化。打印报告显示故障前高压侧负荷电流二次值为2.04 A，CT变比为300/5，所以约为0.74In。故障后三相电流的基波值分别为IA=5.27 A,IB=2.27 A和IC=3.83 A，变压器高压侧中性点未接地，故3I0=0。
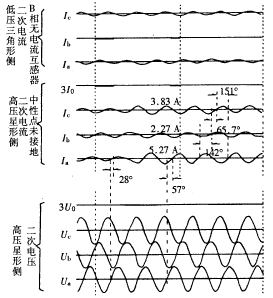
图1 开封滨河变1997年5月6日 高压A相匝间短路录波图
事故前功率因数较高，假设cos?φ=0.9,从录波图上量出?φ=28°,说明假设合理。由于高压侧中性点未接地，A相匝间短路引起的故障分量电流ΔIA只能由B，C相流回，因此有
。假设ΔIA落后UA 80°，可作出三相电流的相量图(如图2)。从图2可得IA=ILA+ΔIA=5.27∠-60°A;IB=ILB+ΔIB=2.27∠-198°A；IC=ILC+ΔIC=3.83∠-263°A。此结果与打印报告中电流的幅值和从录波图上量出的相角十分接近，故假设IA落后UA 80°是正确的①。从图2可测量出ΔIA=4∠-80°A，约等于变压器的额定电流1.45In。 电流的故障分量即继电器的差动电流， 但为了校正Y/Δ变压器两侧电流相位， 差动继电器测量的差动电流应是高压侧两相故障分量电流之差， ΔIAB=ΔIA-ΔIB=2.17In∠-80°， ΔIBC=0， ΔICA=-2.17In∠-80°。两相电流差的额定值为
In,所以此时差动继电器测得的差动电流相当于额定值的
125%。事故时变压器差动继电器的启动电流的整定值为0.5In，因而能灵敏地动作。
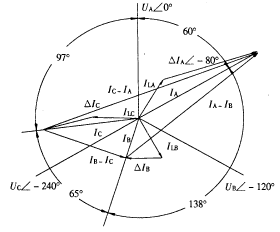
图2 根据录波图作出的三相电流的相量图
这次事故至少引发出以下三个问题，值得我们思考。 (1) 差动保护能够保护轻微匝间故障。长期以来在我国广泛应用由速饱和变流器供电的机械型差动继电器。其有两大缺点：最小启动电流必需大于1.5In才能保证避开励磁涌流，因而对轻微匝间短路不灵敏；当短路电流中有直流分量时动作速度变慢，越是加强速饱和变流器的作用带来的延时越长。若故障靠它切除变压器烧损得十分严重。若有很好的涌流闭锁元件，差动继电器就可以灵敏地、快速地动作，把变压器故障烧损的程度限制到最小，开封滨河变的事故已证明了这种可能性。 (2) 轻微匝间短路时保护能测量到的最小差动电流有多大?轻微匝间短路时测量到的差动电流肯定比在变压器低压侧引线上短路时小得多。错误地用后者作为校验差动保护灵敏度的标准也是造成差动保护不能在匝间故障时起保护作用的原因之一。开封滨河变事故时的故障电流水平有无普遍意义?轻微匝间短路时的最小差动电流如何确定?这些问题需研究解决。 (3) 如何选择制动特性。轻微匝间短路时，一方面故障电流小保护的差动电流就小；另一方面三相电压正常，可继续送出满负荷电流。负荷电流是穿越性的，将产生制动作用，于是很自然要问在此制动作用下，继电器能否动作?我们应当选择什么样的制动特性? 以下对差动继电器能否在轻微匝间短路时起保护作用的问题进行进一步分析。
2 变压器匝间故障的计算 变压器绕组的故障都属于匝间短路故障。以Y/△接线的双绕组变压器在高压星形绕组发生匝间短路为例，把短路绕组和高压绕组分离开来(健全相相应的部分也如此)，于是故障后的变压器变为一个Y/Y/△接线的三绕组变压器(当然高压绕组的匝数减少了)，故障发生在短路绕组一侧的引线上。由此可见匝间短路有多相与单相之分。最常见的尤其是轻微匝间短路都是单相的。为了节省篇幅仅讨论单相匝间短路。 图3示出计算用系统图及在变压器高压绕组发生单相匝间短路的复合序网图，变压器被看成是三绕组变压器，其等值回路是由三个漏抗ZH，ZL，ZK按星形连接的回路。H，L，K分别表示高压侧、低压侧及短路绕组侧。Z1LD和Z2LD为低压侧的正、负序负荷阻抗。高压侧中性点接地时刀闸S闭合，否则S断开。计算的困难在于确定变压器等值回路中的三个漏抗ZH，ZL，和ZK。
图3 单相匝间短路计算用 系统图及复合序网图
变压器绕组的漏抗决定于漏磁通所经路径的磁阻，而漏磁通的路径十分复杂(以下的计算参考文献［2］)。但是在故障前的漏抗是已知的，只要分析出短路后各绕组与原绕组的关系就可近似地得到故障后形成的三绕组变压器的各侧漏抗。 众所周知，对于三绕组变压器通过试验或计算只能依次求得两个绕组之间漏抗，如ZHK，ZHL和ZLK。把它们归算到同一侧如高压侧，那么图3中星形等值回路中的各阻抗为
式中 ZΣ=ZHK+ZHL+ZLK。 从滨河变故障录波分析知道ΔIA落后UA 80°，说明漏抗中有效电阻的成分很小，以下计算中都忽略电阻以漏电抗代替漏阻抗。 为了简单，假设绕组是圆筒形的。圆筒形绕组的漏磁通的路径有效长度决定于绕组的高h和有效厚度d。通常在计算时把厚度折合为高度得到磁路的有效高度或有效长度h′=kh,其中k是折合系数，一般k=1.1。显然k与比值 (1) 高压绕组和短路绕组之间的漏抗X?HK。绕组的漏抗与匝数的平方成正比，与磁路的有效长度成反比。高压绕组去除短路绕组后的匝数，与短路绕组匝数占原来总匝数之比分别为1-α和α。这两部分圆筒的半径相同，是叠起来的，它们之间的漏磁通不穿过铁芯，全部在空气中形成环路，有效高度要加大一倍。短路绕组漏抗将是 (2) 高低压绕组之间的漏抗XHL。绕组的漏抗与漏磁通路径的截面成正比。在绕组直径一定时截面与绕组等效厚度( 已知的Xσ是原来两个绕组漏抗的和，与Xσ相对应的漏磁通占据了整个截面。在上面计算XHK时因为每一绕组的漏磁通都占据了整个截面就直接以Xσ为基准进行计算。现在计算XHL就必须注意到漏磁通路径截面在两个绕组间的分配。 现高压绕组的匝数和高度都减少了，整个绕组都面对着低压绕组，它的漏磁通路径的截面应减少一半，计算时所用的基准电抗也应减少一半。所以高压绕组的漏抗为 (3) 低压绕组与短路绕组之间的漏抗XLK(归算到高压侧的值)。短路绕组都面对低压绕组，所以计算的基准电抗要减少一半。其归算到高压侧的值为 求出XHK，XHL，XLK后就可求出图3中等值回路中的XH，XL，XL。 表1示出对于几个不同α值计算得到的漏抗(相对于Xσ)之值。
有关。短路绕组的高度等随着短路匝数而变化，其折合系数也要随之变化。为了简化，下面取实际高度ht与有效厚度d=0.1ht之和作为磁路的有效长度h′，ht为原来整个绕组的实际高度。于是如果短路绕组匝数占原高压绕组总匝数之比为α(1＞α＞0)，则短路绕组的实际高度为αht。短路绕组的漏磁通的路径的有效长度与原有效长度之比为
。设变压器原有的漏抗为Xσ。以下依次计算三对绕组之间的漏抗。
，其归算到高压侧之值为
。同理高压绕组的漏抗为
。于是可得
。
)成正比。γ为两绕组之间气隙的宽，γ1和γ2分别为两绕组的厚度，漏磁通的一部分仅与高压绕组相连，另一部分仅与低压绕组相连，它们分别决定每一绕组的漏抗。要求每一绕组的漏抗，必须确定这两部分漏磁通在空间的分界线，这是困难的。试验也无法确定每一绕组的漏抗。计算时一般认为两绕组的漏抗(归算到同一侧的值)是相等的。
。低压绕组完好如初，匝数和高度都没有变化，但一部分(1-α)WL面对高压绕组，其余αWL则否。前一部分产生的漏磁通的路径的截面应减少一半，后一部分则否。因此低压绕组的漏抗(归算到高压侧的值)应为
。于是可得
。低压绕组的一部分αWL面对短路绕组，其余部分则否。它归算到高压侧的值为
，所以低压绕组与短路绕组之间的漏抗(归算到高压侧的值)为
表1 变压器匝间短路不同α值下的等值回路参数
| α | 0.01 | 0.025 | 0.05 | 0.1 | 0.2 | 0.5 |
 |
2.17 | 1.67 | 1.11 | 0.67 | 0.42 | 0.25 |
 |
-1.18 | -0.69 | -0.16 | -0.22 | 0.35 | 0.17 |
 |
7.05 | 5.81 | 4.35 | 2.77 | 1.4 | 0.25 |
| 由表1可见在α＜0.2时都有(XH+XK)/Xα＞1。在这些匝间短路时的短路电流都将小于在低压侧引线上短路时的电流。差动保护绝对不能用后者校验保护的灵敏度。 从表1还可以看出α越小XHK=XH+XK越大。 由于计算依据的主要参数——故障变压器的漏抗和负荷阻抗都是近似，所以没有必要作严格的计算。由图3可见系统供电到P1点后分为两个支路。一是经低压侧漏抗向负载Z?1LD供电，另一是经短路绕组漏抗向零序、负序网供电。这两个支路的阻抗角相差很大，并联计算很烦。粗略分析认为它们分别独自存在，即分别计算负荷状态和空载时的故障状态。前一种状态下得到穿越性的负荷电流，后一种状态下0，1，2三个序网串联，串联的总阻抗约为3(ZH+ZK)。差动保护测量的是两相电流之差，不反应I0，不论变压器中性点是否接地都有I1=I2，不考虑I0有IA=2I1,IB=IC=-I1。由此得I?AB=I?CA=3I1,IBC=0。由于正常时两相电流差是相电流的 表2 不同Xσ值下差电流的标么值 |
。对于不同Xσ值，变压器轻微匝间短路时保护测得的差动电流的标么值示于表2。 | Xσ | 0.08 | 0.11 | 0.14 | |
| Id* | α=0.01 | 0.78 | 0.56 | 0.45 |
| α=0.025 | 0.96 | 0.70 | 0.55 |
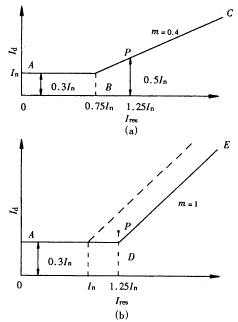
| 滨河变高压线组共约30层，一层中约3/10匝短路。计算时认为短路绕组的高度降低为原绕组的α倍，厚度不变，当然有误差。滨河变在故障时Id*=1.25In，表2计算为Id*=0.78In,可见计算结果有误差。 根据以上估算在校验变压器对轻微匝间短路的灵敏度时可取穿越性电流为In，差电流为0.5In，并认为两者相位相同。 3 比率差动继电器动作特性的选择 比率差动继电器的动作特性Id=f(Ires)一般是折线，如图4所示。折线由与Ires轴平行的直线和斜率为m的直线两部分组成。折线拐点位置有两种取法。第一种取法所得折线如图4(a)中的ABC，第二种取法所得折线如图4(b)中的ADE。水平线与Id轴的交点A的纵坐标I0为继电器的最小动作电流。图4(a)中斜线BC经过坐标原点，拐点B由I0和m决定。图4(b)中拐点D的横座标一般取Ires=In如图中虚线所示，其出发点是认为在穿越性电流Ires小于负荷电流In时差动保护的误差很小，不需要制动作用，继电器就是简单的差动电流继电器。
图4 二种折线型比率差动继电器的动作特性 制动电流Ires的取法很多，但共同之处是都认为在外部短路时Ires等于或正比于(一般为2倍)穿越性电流。实际不同取法并无重大差异。对于双绕组变压器，应用最广范的是取Id=｜I1+I2｜和Ires=｜(I1-I2)/2｜。I1和I2是变压器两侧的电流，以流入变压器为正方向。 在讨论选择和整定制动特性之前，作者愿意重申在文献［1］中提出的2个观点。一是在外部短路时误差不仅产生不平衡的差动电流，而且也使制动电流减少，不再等于穿越性电流。后者往往被忽视。例如当采用图4(a)的制动特性Id≥mIres时一般都认为m=k?res就表示外部短路时允许的误差，其实不然。将Id和Ires用I1和I2表示，在外部短路时I1和I2相差180°，故有Id=I1-I2和Ires=0.5(I1+I2),代入式Id=mIres后便可求得δ=(I1-I2)/I1=2m/(m+2)。表3列出不同m值时的δ值。由表3可见误差使制动电流减少的影响不可忽视。二是在选择制动特性时迄今的做法是使制动特性最大限度地靠近外部短路时不平衡差动电流的区域，从而在内部短路时可获得最大的灵敏度。作者建议反其道而行之，按保证在内部短路时能够动作的条件选择较大的制动系数，从而在外部短路时获得最大的选择性。作者认为在内部短路时只要没有穿越性电流流过就不会有制动作用，Id/Ires的最小值是容易确定的。尤其是数字式继电器只要Id和Ires是由同一数据采集系统采集到的，那么比率制动判据就一定能满足。这样做的好处是可以免去计算外部短路时不平衡电流的麻烦，从而得到通用特性。详细见文献［1］。 表3 制动特性为Id＞mIres时δ和m的对照 |
| m=kres | 0.20 | 0.30 | 0.40 | 0.50 | 0.66 |
 |
0.18 | 0.26 | 0.33 | 0.40 | 0.50 |
| 现在根据轻微匝间短路的要求选择图4中的动作特性。首先由于轻微匝间短路的最小故障电流可能为0.5In，因此选择I0=0.3In是适合的。如果采用浮动门槛技术则可进一步提高灵敏度。再考虑在轻微匝间短路时可能送出满负荷电流，即I1=1.5In，I2=In，则有Ires=1.25In,所以应使轻微匝间短路时的工作点P(1.25In，0.5In)落在动作区。如果采用图4(a)的特性应取m≤0.4，由表3可知允许的误差δ≤0.33。如果选用图4(b)的特性拐点D，最好在Ires=1.25In的地方，这样在轻微匝间短路时没有制动作用，得到最大的灵敏度。 按照文献1的观点，图4(b)中直线DE的斜率m=1。现在拐点D的横坐标Ires=1.25In,DE的直线方程为Id-Ires+0.95In≥0。分析外部短路时允许的误差只要将Id=I1-I2和Ires=0.5(I1+I2)代入，可得I1-3I2+1.9In≥0。于是可求得在不同I1值下允许的I2的最小值，进而求出最大的允许误差δ=(I1-I2)/I1，示于表4。 表4 通用比率制动特性在外部短路时允许的误差 |
| I1/In | 1.5 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| δ | 0.244 | 0.350 | 0.455 | 0.508 | 0.540 | 0.603 | 0.624 | 0.635 |
| 显然图4(b)的特性比图4(a)优越。比率差动继电器采用这样的特性和整定值可以适用于任何系统中的任何变压器，所以称为通用特性。 突变量差动继电器保护轻微匝间短路有显著的优点。在突变量差动继电器中差动电流和制动电流都是突变量，即ΔId和ΔIres。轻微匝间短路时流过的穿越性负荷电流分量不会反映到ΔIres中去，因而提高了灵敏度。其比率制动判据可采取图4(a)的特性。在正常时Id=0，差动电流本身就是故障分量，但动作电流仍然要用突变量ΔId,否则在外部短路尚未被切除前ΔIres已消失而差动不平衡电流Id却仍然存在，将失去选择性。在外部故障发生时ΔIres应在ΔId之后消失。有关问题在文献［1］中已阐述，这里不再赘述。 顺便指出，按本文提出的要求，标积制动原理并无优点可言。 4 有关灵敏度的几个问题 (1) 比率差动继电器采用通用特性，最小启动电流I0=0.3In,对变压器低压引线上的故障肯定足够灵敏。对内部轻微匝间短路用什么标准校验呢?本文对匝间短路的估算和开封滨河变的事故足以证明在α=0.01的轻微匝间故障时系统电压保持不变，可继续带负荷，而且变压器损坏较轻，易于修复。所以更轻微的故障保护若不能立即动作也不会有严重后果。变压器事故造成的损失包括对系统造成的损失和变压器本身损失。故障一开始保护未动，等待故障发展到α=0.01时再动作，给系统造成的损失是相同的，变压器的损失也相差无几。故障是发展了，事故几乎并未扩大。保护的过分灵敏必然要降低安全性和选择性。所以作者认为采用本文推荐的通用特性在一般情况下已足够灵敏。如果还要进一步提高灵敏度，则以采用突变量差动继电器为宜。 (2) 图1的录波显示电压正常，负荷不变，说明轻微匝间故障时短路匝电流的去磁作用可以忽略，在变压器合闸于匝间短路时很可能同时出现涌流。涌流判别元件会短时闭锁保护，但增加的延时不会长，由于故障轻微，不大的延时应当是可以容忍的。 (3) 为了在一相有故障，另一相有涌流时能快速切除故障，采用涌流判别元件按相闭锁差动继电器。但在无故障合闸时可能因一相涌流特征不明显而未能实现闭锁。为此可采取两相继电器动作才出口。分析表明单相匝间短路与低压侧两相短路一样将有两相继电器动作。在微机保护中三相继电器都用同一CPU所执行的程序完成，所以当两相继电器都应动作时不会出现一相动另一相拒动的情况。在轻微匝间故障继电器可能处于动作边界时，可能只有一相动作，但由于故障轻微危害不大，等故障发展后再切除也是允许的。 ①作者在文献［1］中认为：由于故障处的电弧电阻限制了短路电流导致ΔIA和UA基本同相是不正确的。 |
