考量运算放大器在Type-2补偿器中的动态响应(二)
在本文的第一部分,我们讨论了当运算放大器用于type-2补偿器时,对开环增益AOL的影响。对运算放大器幅值和相位响应的进一步分析,显示存在低频和高频两个极点。如果在低带宽设计中可忽略这些极点的存在,那么在高带宽系统中需要增益和相位增强时就必须考虑它们带来的失真。第二部分中将讨论由于存在这些极点,如何确定type-2补偿器的传递函数以及它们将怎样令滤波器性能失真。
运算放大器中的两个极点
为了稳定运行,运放设计人员实施所谓的极点补偿,包括在低频放置一个极点,使放置第二高频极点前在频率fc处的增益下降到1(0dB),通常在2fc.。
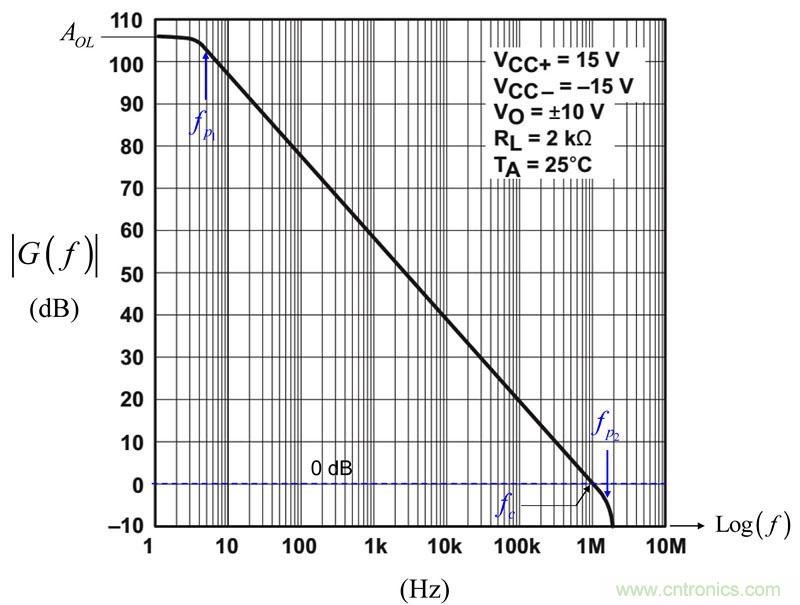
图1:运放的开环动态响应揭示了两个极点的存在
图1所示为一个典型的μA741,您可看到交越频率1 MHz,低频极点5 Hz左右,而第二极点出现在2MHz。请注意,这是个典型的响应,开环增益AOL106dB。开环增益不是个精确控制的参数,它可显着变化。数据表规定在整个温度范围内(-55至125°C)增益从15K(83.5分贝)移至200K(106分贝),那么当分立时,这曲线转变。
一个简单的拉普拉斯表达式可描述这两极点开环响应,如图1所示:
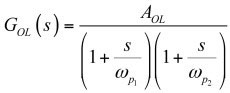 (1)
(1)
由图2的Mathcad?绘制曲线确定:
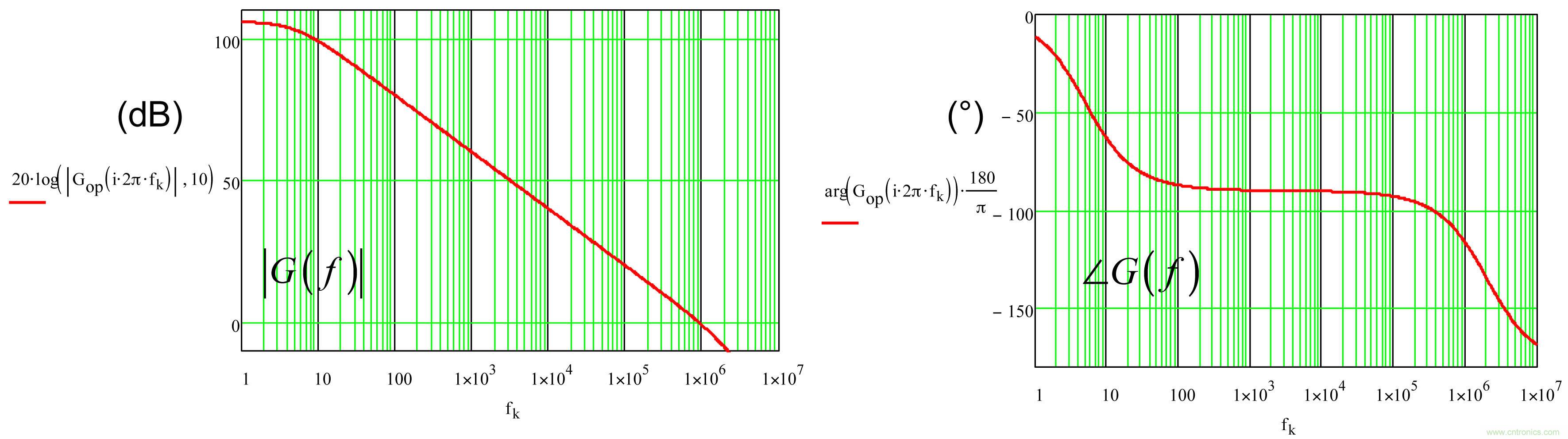
图2:运算放大器有一个低频极点,第二极点在超过0dB的交越频率处。
运算放大器的一个简单的SPICE模型
我们可以很容易地建立模仿图2的频率响应的SPICE模型。如图3,它采用一个电压控制的电流源G1,G1有跨导gm,后连一个接地电阻ROL,再与电容C1并联。对于ROL,反相引脚Vinv的传递函数很简单:
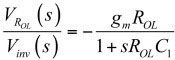 (2)
(2)
如果我们现在缓冲电压,并放置具有电阻R2和电容C2的第二极点,我们得到我们想要的完整的传递函数:
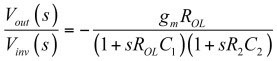 (3)
(3)
元件值已自动显示在页面的左侧,一旦运行仿真,右侧就显示所获得的幅值/相位图。这是个简化的运算放大器模型,但它可以用于第一阶分析。它可稍后升级到模型更特定的特点,如电压钳位或压摆率电路,如 [ 1 ] 所描述的。请注意图中LoL和CoL的存在,由于它们的存在,在元件运行开环时需要将运算放大器输出电压固定为2.5 V。这里因为没有电源轨,我们可运行一个简单的交流分析,不考虑直流偏置点。
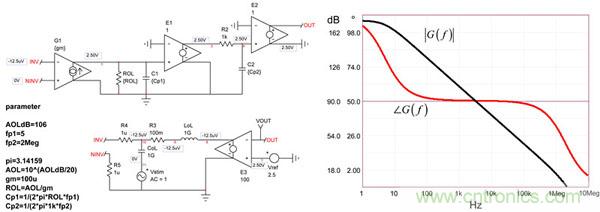
图3: 一个简单的SPICE电路,可建立一个有开环增益和两极点的运算放大器。
然而,如果您打算分析一个包括电源轨的更全面的模型响应,那么当您想要手动调整直流工作点时,这个简单的电路将避免该集成电路上下波动。在仿真开始时LoL短路,有助于以E3和源Vref调整工作点。一旦交流扫描分析开始于CoL,LoL阻断E3的调制,调整工作点的电路转而静止。这是通常的诀窍,采用平均模型以运行开环增益分析,同时确保确定闭环偏置点到所需的输出值。这个简单的SPICE模型将帮助测试我们分析得出的数学表达式。
Type-2补偿器有两极架构
既然我们知道运算放大器有两个特别的极点,我们可更新在本文第一部分我们最初使用的草图。图4所示为新建立的type-2补偿器,现在包括运算放大器的内部特征。
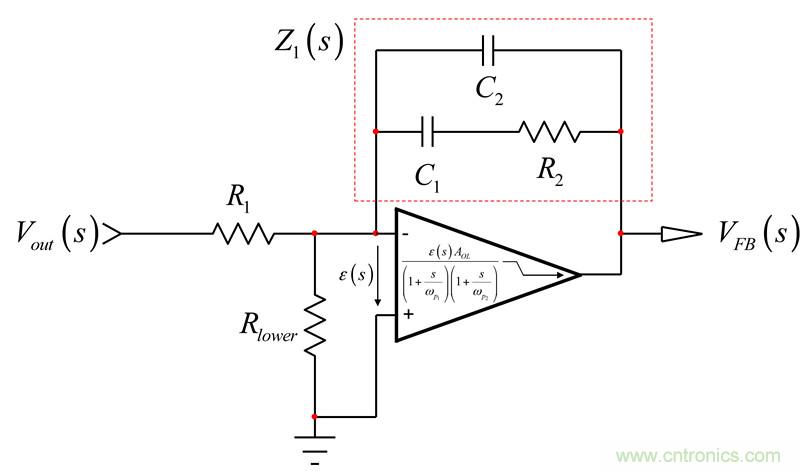
图4:更新电路将运算放大器中存在的两个极点考虑进来
输出电压VFB是误差电压?乘以运放的开环传递函数
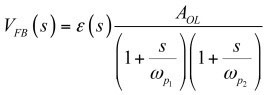 (4)
(4)
另外,误差电压可通过使用叠加定理将Vout和VFB设置为0V得出:
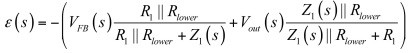 (5)
(5)
如果我们将(5)代入(4)并加以整理,得出:
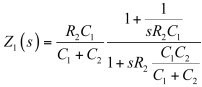 (6)
(6)
Z1(s)相当于:
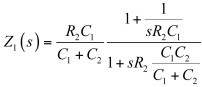 (7)
(7)
请参阅本文结尾的附录,以了解如何用快速分析技术以简单的步骤推导出这个表达式。
这个方程极其难处理,但有利的是,对于Mathcad?不是问题。我们可通过比较其动态响应与SPICE模型以验证它是否正确。我们假设下列元件值:
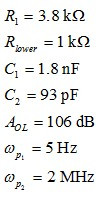
采用type-2架构的SPICE电路如图5所示。
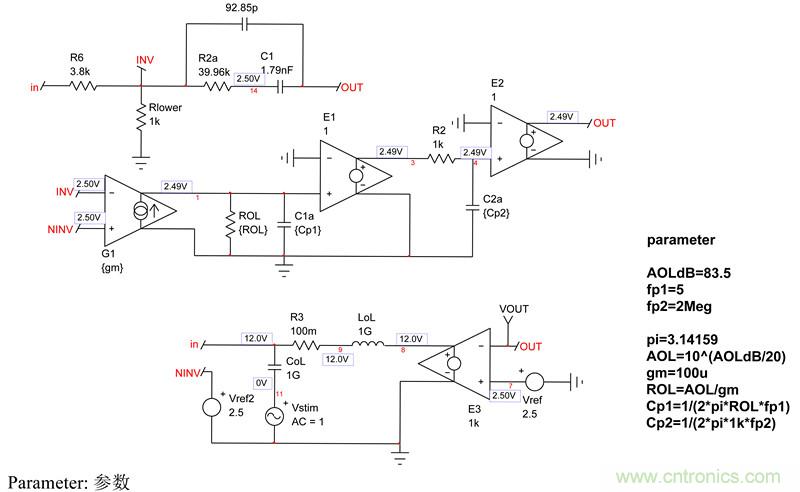
图5:完整的type-2 SPICE模型现在构成运算放大器的动态响应。请注意,考虑到2.5V参考电压Vref2现在偏置于NINV引脚,将直流偏置点设置为12V。
由图6证实,Mathcad?和SPICE之间的响应是相同的,确定方程的有效性。
特征失真
图5仿真采用的元件值来自一个type-2补偿器,旨在以20dB的增益在10kHz交越频率处建立65°相位增量。如果我们现在比较由本文第一部分方程(36)给出的理想的type-2响应与使用μA741 (106dB AOL,有两个极点,5Hz和2MHz)的type 2电路的响应,您会注意到一些差异,如图7所示:
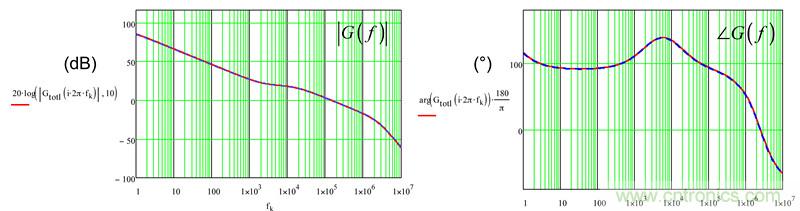
图6:由Mathcad?提供的绘制曲线与由SPICE产生的曲线完美重合
在该图中,我们可看到在10kHz处有轻微的增益偏差和离20dB差约2.2dB。其实无关紧要。而更重要的是您以完美的公式实现期望的65°相位增量。在10kHz处,由具有真正运算放大器的电路提供的相位增量仅44.6°或相差20.4°。这将相应减少最终的相位裕量。
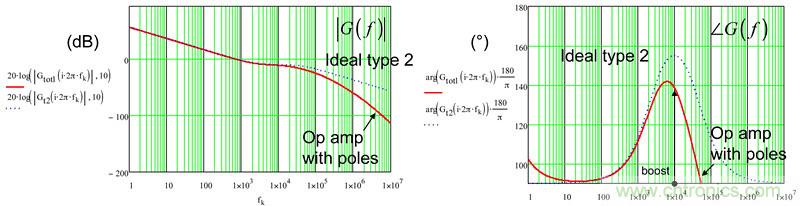
图7:用有最高开环增益的μA741创建type 2,已导致相位增量失真。
但后面更糟糕。如果您考虑由数据表显示的开环增益的偏差,若AOL降至83.5dB,最小的规格是多少?图8证明:在10kHz处的20dB增益差17dB,而相位增量骤降至6.7°。无需解释为何系统的稳定性与最后一个值有关。图9的SPICE仿真通过在同一图中采集的3条不同曲线确定了这些数据。您可看到开环增益偏差的不利影响。
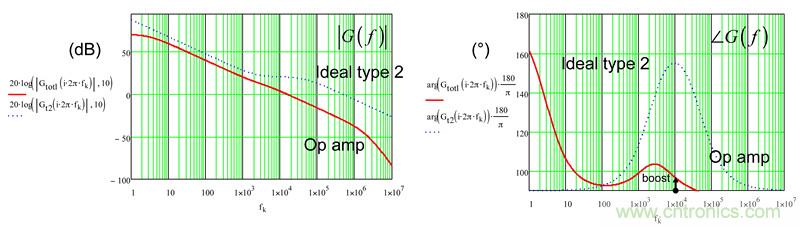
图8:如果开环增益现在骤降至83.5dB,如运算放大器数据表所述,相位几乎无提升。
如果我们现在改变type-2规格,也就是说我们在10 kHz处不再需要一个增益,但在fc 处有10dB的衰减,同样相位增量65°,相位增量失真不那么明显,开环增益较低(见图10)。
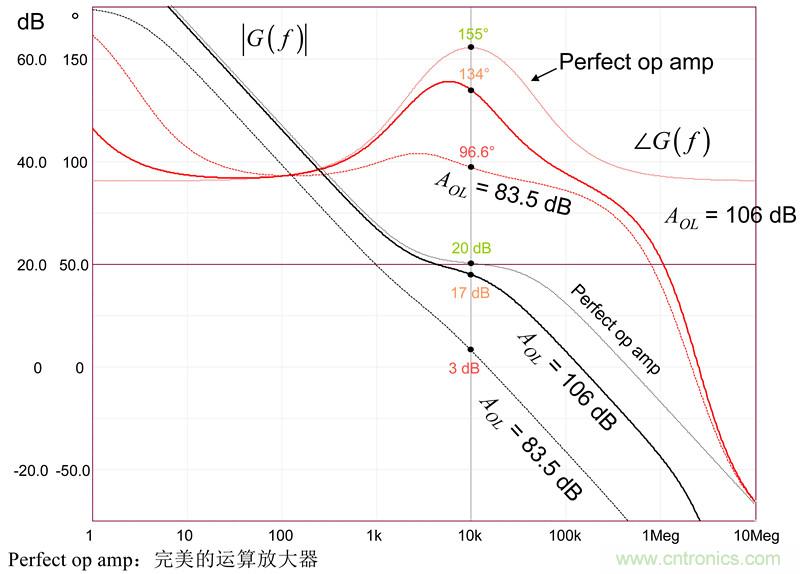
图9:运算放大器开环增益的变化引起严重的增益/相位失真
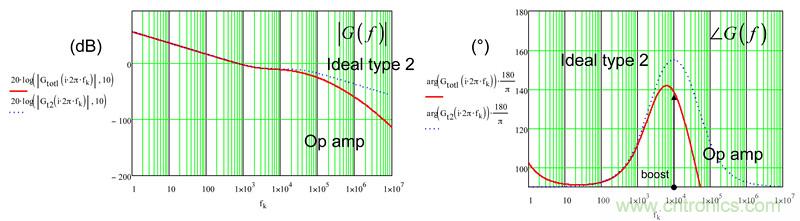
图10:如果type-2电路改为以10dB衰减而不是在相同的10kHz交越频率处放大,目标仍没有达到,但失真程度较小。
采用此架构获得的中波段增益是-11dB(相对于-10dB的目标),而相位增量刚达到49°(相对于原来的65°目标)。
Type-2响应和开环增益绘制曲线
为确保运放内部不改变补偿器响应,通常的建议是在相同的图线上叠加理论型type 2幅值和运算放大器开环响应。在图11中,左图对应于我们第一次尝试建立的一个type 2补偿器,在10kHz处有65°相位增量和20dB增益。在该图中,运放幅值与type 2补偿器相交和相悖,导致我们想要的特征被破坏(最终的相位误差几乎有60°)。一看就很明显,这交叉表明,要么是选择的运放不适合,要么用type-2补偿器设置的目标过高。
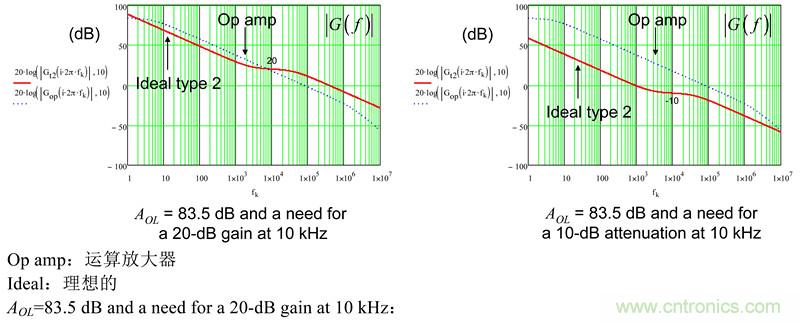
图11:左图清楚地显示这两个响应相交和衰减。右边的幅值图中没有交叉,但最终的结果也失真。
图11的右图似乎表明,我们应当可以设计那样的type-2电路,在10kHz交越频率处不再有增益而是衰减。但我们的计算表明不是这样,因为确定最终有17°相位误差。
一种方法建议选择一个增益带宽乘积(GBW)大于所用type 3补偿器的0dB交越频率的运算放大器。然而您可看到,它不适用于图11:在左边,type 2的0dB交越频率400kHz左右,而在右边,我们想要衰减而不是增益。我提出一个稍微不同的经验之谈的方案,其中运算放大器的开环响应必须比type 2补偿器的20fc “飞高” 20dB。如图12所示。图形化的方法是确定你的运放必须具有多少GBW的第一步,以使所需的相位增量和增益目标在可接受的范围内。
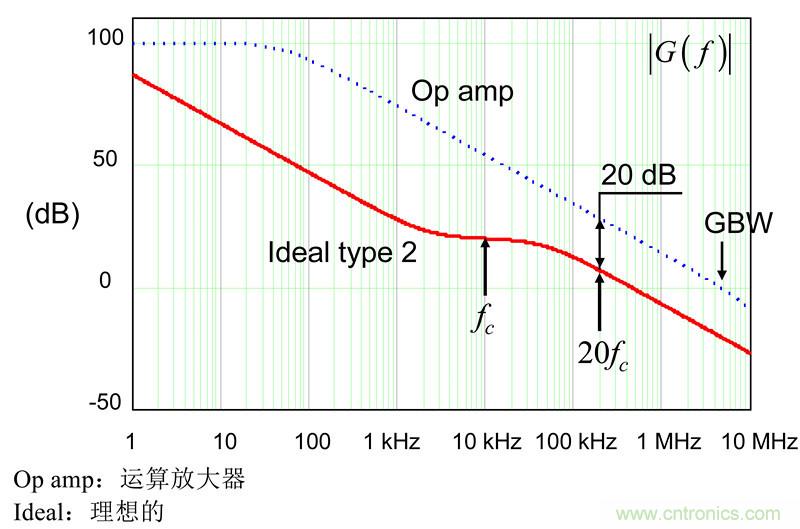
图12:作为第一步,我们建议选定运放的开环响应至少比type 2补偿器的second -1-斜率高20dB。
您首先计算type 2在20fc处的dB幅值,再加20dB。然后您计算出相应的运放开环增益交越频率或GBW:
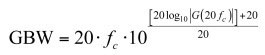 (8)
(8)
图11的左边,(8)给出了4.4MHz的 GBW,而对第二种情况建议150kHz的GBW。应用这一策略到第一个例子,从而选定运算放大器开环增益为90dB,低频极点位于150赫兹,或开环增益80dB,低频极点450赫兹。不要减少开环增益到70dB以下,以使稳态误差在可接受的范围内。当应用这种策略,中带增益为19.5dB,相位增量约60°?。在第二个例子中,(8)建议GBW 140kHz,开环增益80dB和低频极点15 Hz。中带增益色散为0.4dB,相位增量为56°或偏差9°。低频极点增至30赫兹,降低增益色散到0.2dB和相位增量误差为4.4°。
有了公式(8),您可开始选择一个合适的运放的GBW。基于观察和反复实施几种情况以找到合适的GBW。我曾试图从(6)提取可能的GBW–例如忽略高频极点作用–以符合最初完美的type 2特定的偏差,但我不确定已经确立有意义的表达式。一旦您有建议的GBW,就能查找运算放大器的数据表和确定一个合适的元件。将AOL和低频极点与Mathcad?表[ 3 ]联系起来,比较与目标的偏差。一定要探索最小值,以致在最坏的情况下偏差仍是可接受的。
高频电流模式降压转换器的补偿实例
假设我们设计了一个5A降压稳压器,将3.7V电池降至1.5V,开关频率1MHz。输出电容是180μF和有3m?等效串联电阻(ESR)rC。假设我们想要50mV输出压降,负载变化从1.5A到5A。因此电源输出阻抗必须等于:
![]() (9)
(9)
这可能表明小信号的闭环输出在交越频率fc处的阻抗以电容器阻抗为主,其提供的ESR足够小:
![]() (10)
(10)
从所需的压降,考虑180μF电容和想要的14.3m?输出阻抗,我们可估算出需要的交越频率是:
![]() (11)
(11)
有些人会反对,认为这是对小信号的近似分析,大信号响应将不同。这是事实,但经验表明,最终的结果与计算相近。当然,当存在ESR和ESL(寄生电感),结果大大不同,但这第一阶的方法是个有意义的起点。此外,此方法分析表明将交越频率与通常建议的Fsw/5或Fsw/10相比,往往是荒谬的。
我们选择了62kHz的交越频率fc。为了补偿这种转换器,我们首先需要功率级的动态响应,这是分析的出发点。有几种方式:a)使用控制到输出的传递函数H(s)并由此得出波德图)b) 用平均模型建立一个仿真设置 c)在实验室建立一个原型和用网络分析仪提取响应 或d)用Simplis?或PSIM?建立开关模型和提取交流响应。我们采用了策略b)如图13所示。
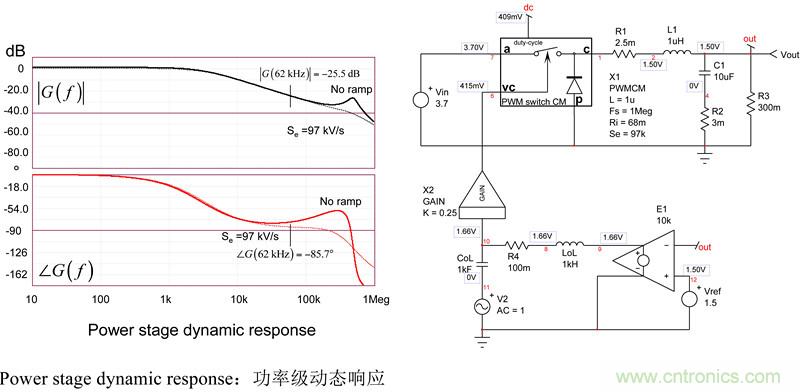
图13:平均模型帮助我们很快建立电流模式转换器
从幅值图,我们看到,如果我们想要62kHz交叉频率,中频带增益必须是25.5dB。如果我们目标是70°相位裕度(pm),在交越处约86°的相位滞后(pfc)需要以下相位增量值:
![]() (12)
(12)
从Mathcad?表的计算表明,一个极点位于291kHz,而零点将位于13.2kHz。根据(8),必须选择一个50 MHz的GBW放大器。查阅各种运放的数据表,我们发现LT1208具有典型的7k开环增益(约77dB),可降到2k(66dB)为最小值。其典型增益带宽积为45MHz,在电源?5V时,降至34兆赫。因此,低频极点位于34兆赫/7k,约4.8kHz处。
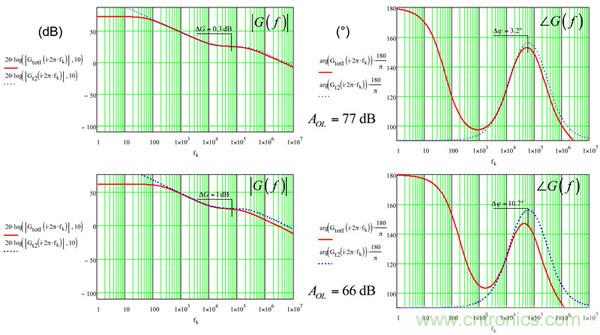
图14:开环增益色散会影响到最终有效的相位增量
图14所示为两个不同的开环增益的type-2波德图。77dB提供45 MHz GBW和色散很小。当AOL降至66dB(最低规格),增益色散仍可接受,但相位增量偏离目标10.7°。
降压转换器中的运放
我们现在可以实际模型(至少有AOL与两个极点)闭环和捕获选定的运算放大器的特点到我们现在更新的的仿真原理图。
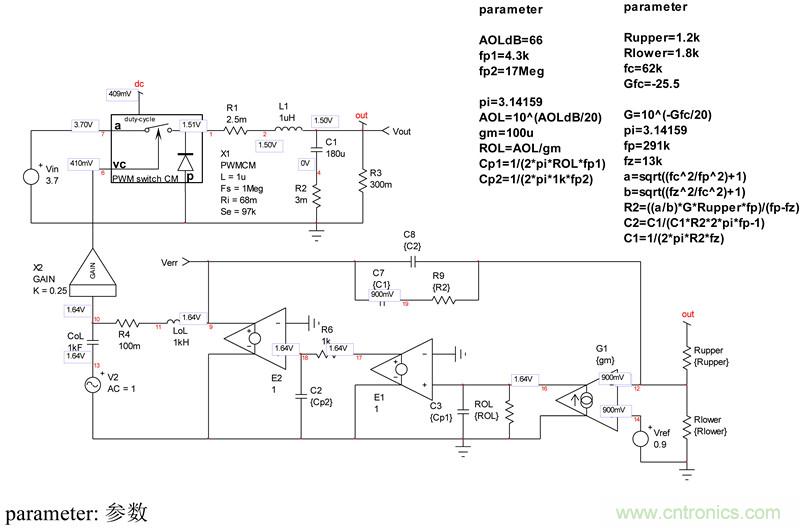
图15:运算放大器现在有低频和高频两个极点
由该图,我们可绘制开环增益T(f),并看到开环的变化如何影响动态响应。结果如图16所示。正如预期的那样,交越频率和相位裕度出现一些色散。
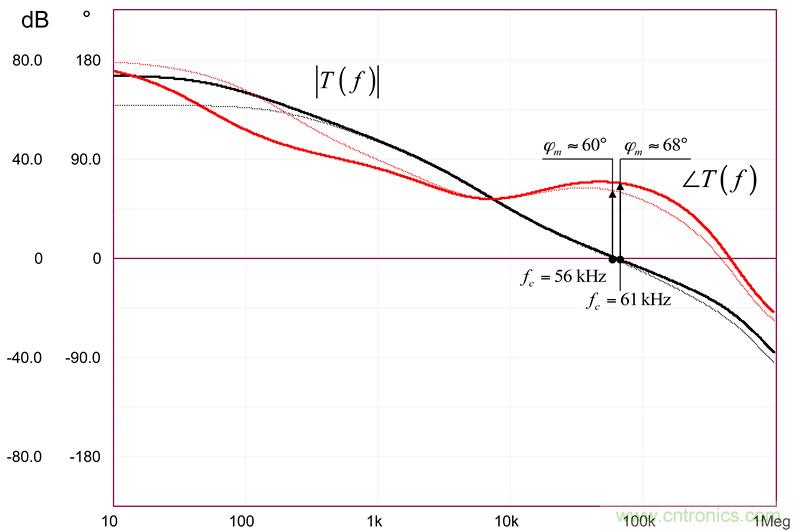
图16:动态响应受开环增益变化的影响。在最坏的情况下(66dB AOL),相位裕度下降到60左右°,是可接受的(虚线)。
由图15仿真电路,我们可运行一个瞬态负载阶跃,并检查两个不同开环增益的响应。结果如图17所示。
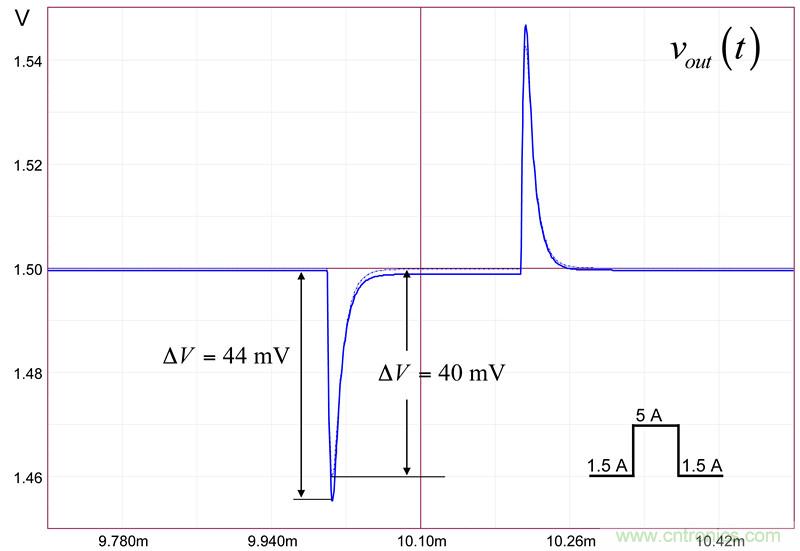
图17:最低的开环增益有44mV的偏差而典型值导致压降40mV(虚线对应于66dB AOL)
该压降在两个开环增益值的规格范围内。当然,这是个简化的方法,考虑到运算放大器的误差电压偏差(1.6 V),压摆率必须是整个分析的一部分,其影响对瞬态响应的评估。
总结
第二部分介绍了运放动态响应对补偿器性能的影响。当需要大带宽时,您不可再忽视这些对补偿器的动态响应的作用。可以将您想要的完美的type-2响应与所选择的运放的开环幅值图叠加,并看看是否重叠。然而,我们已看到的一种情况是,不重叠最终导致一个显着的相位增量失真。通过运算放大器开环响应和完美的type 2开环响应之间的显著差距,您可选择增益带宽积,并以给定的公式检查它如何影响所需的响应。一个全面的稳定性分析,必须通过影响所有元件容差考虑整个环路增益,包括运算放大器的内部。通过(6)中完整的type-2传递函数,您就可以进一步分析。
附录 – 阻抗计算
为确定由(7)给出的阻抗,我们可以充分应用快速分析技术。原理图如图18所示。为了获得阻抗,我们将电流源IT注入到电路环路。IT是激励而VT是响应。我们想要的传递函数是将响应与激励联系起来的关系。为了便于分析,我们在测量终端装上了假负载电阻Rinf。我们将马上看到其中的原理。
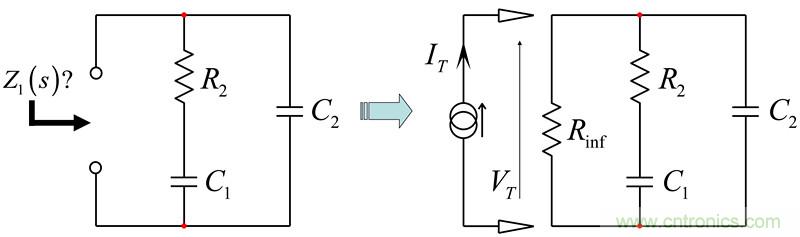
图18:有两个电容,这是个二阶电路。
这类回路的传递函数可表示为以下形式:
![]() (13)
(13)
对于二阶系统,我们可以证明分母遵循下列公式:
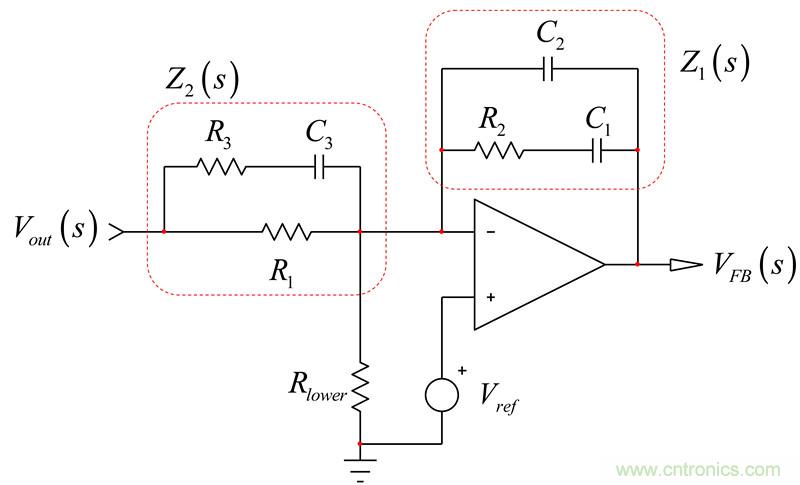 (14)
(14)
?1和?2是所有储能元件(C和Ls )保持在直流状态(电容开路,电感短路)时获得的时间常数。 表示在时间常数1(上标数字)的元件处于高频状态(电容器短路,电感开路),同时确定在时间常数2的元件端的电阻。相反的, 表示在时间常数2(上标数字)的元件处于高频状态(电容器短路,电感开路),同时确定时间常数1的元件端电阻。然后将这些时间常数组合,成为如(14)的D(s)。
首先,我们看看S = 0时,储能元件端的电阻。在直流状态下,我们让所有电容开路和电感短路(如果有的话)。在开始任何类型的分析(.TRAN 或.AC)前,确定偏置点时,SPICE也同样这样做。我们想象如果我们移除电容器,输入端阻抗由Rinf决定,因此它的存在避免了无法衡量的项:
![]() (15)
(15)
然后,我们确定每个电容器端提供的电阻R,而其对应于非直流状态(断开或从电路中移除)。我们绘制出图19。时间常数由?= RC定义。
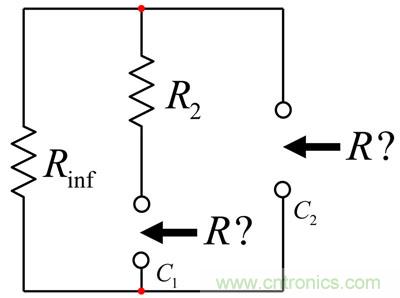
图19:您现在评估每个电容器端在直流状态(从电路中移除)时所提供的电阻
无需写一行代数,我们就可以检查图形和“得出”电容器端的电阻。我们有:
![]() (16)
(16)
和
![]() (17)
(17)
有了直流时间常数,让我们确定更高的频率,如图20所示。对于 ,电容C1短路,您看看电容C2端的阻抗。
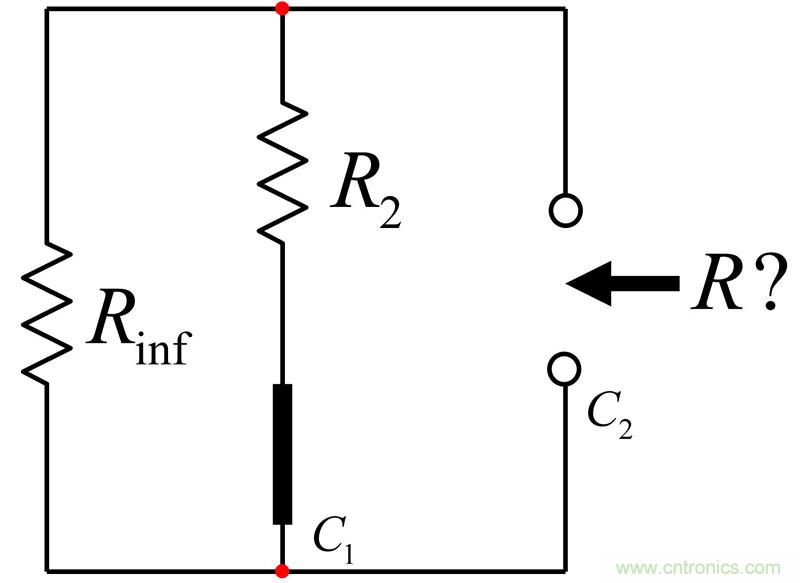
图20:电容C1短路,C2端的电阻是多少?
时间常数直接等于:
![]() (18)
(18)
如果我们评估 ,将发现:
![]() (19)
(19)
我们将所有项组合形成D(s):
![]() (20)
(20)
分子可以通过检验得出。如果您还记得我在第一部分所说的,当一个特定的S值使变换后的回路无响应(即C替换1/SC)时,会找到零点。在图18中,响应是VT,由电流源测量。当VT变为0 V,电路中一定出现了转换的短路。如果是这样,那么:
![]() (21)
(21)
如果是这样,那么:
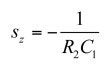 (22)
(22)
一切都已妥当,完整的传递函数如下所示:
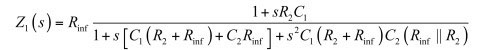 (23)
(23)
在分母中,提出Rinf,得到:
 (24)
(24)
简化,令Rinf接近无穷大。最终的表达式为:
![]() (25)
(25)
如果您现在将分子中的R2C1提出,会得出分子中有倒数的所谓的低熵表达式:
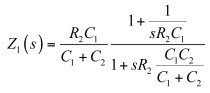 (26)
(26)
可用下列公式进一步调整:
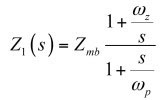 (27)
(27)
![]() (28)
(28)
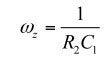 (29)
(29)
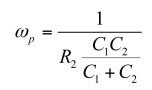 (30)
(30)
首项(28)仍然含阻抗,但不再是S=0时的值。它是您在图21中看到的平坦区或中频带电阻,我们汇集所有表达式来测试它们的个别响应。它们都是相同的。
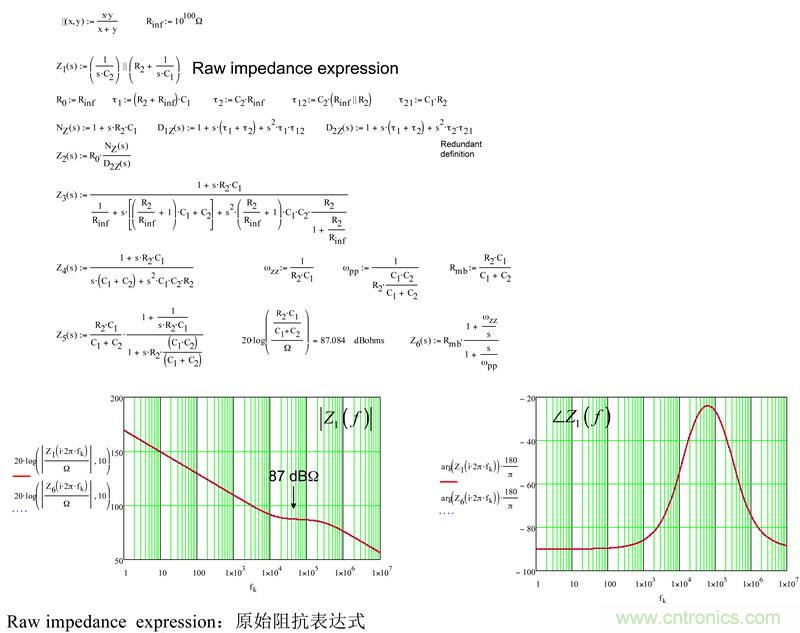
图21:Mathcad?确定原始表达式和最终表达式相同
快速分析电路技术展示了如何将电路分解成小的个别的草图,并单独解决每个草图。若可检测,很快就能得到结果,和得出有条有理的形式。这是这种方法的强大之处,我鼓励您掌握这技巧,因为在确定复杂的传递函数时,时间优势是很重要的。 为激发您的兴趣,请看图22。您看到一个type-3补偿器。无需写一行代数,我可以告诉您,当Z1和Z2分别转化为短路和开路时,响应VFB消失。(26)已评估了Z1,并提供一个零点,等于:
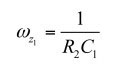 (31)
(31)
为了防止激励Vout形成响应VFB,还有个选择是Z2开路。换句话说,对于s = sz2,阻抗表达式不再有分母。
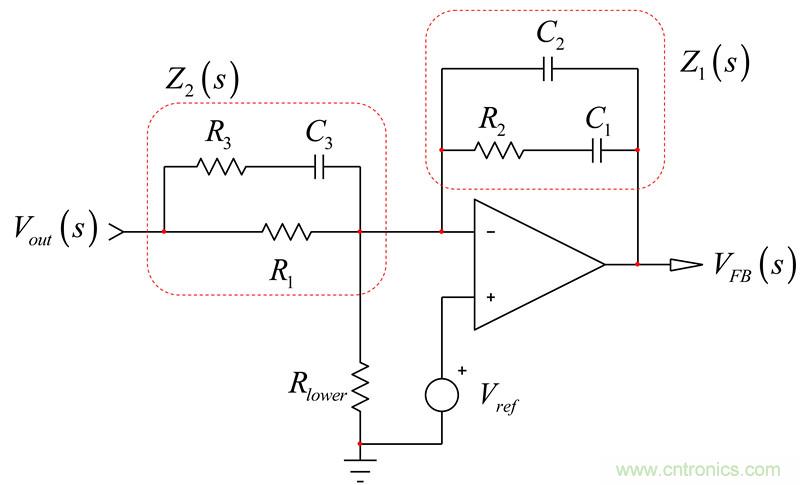
图22:type-3电路是三阶有源滤波器
为确定Z2的阻抗(孤立于整个电路),我们可以想象一个电流源与R1并联,如图18的右图。s = 0时,您“看到”电流源两端的阻抗是R1(C3处于直流开路状态)。当激励(电流源)减至0A(一个0-A电流源从电路消失)时,时间常数是C3两端的电阻R,数倍于C3。简单地表示为 。我们不需要分子,因为我们只对分母的根感兴趣。然而,如果您也想要分子,那么与我们分析Z1的架构相同。如果R3和C3短路,电流源的响应VT消失。只要组合这些数据,就有:
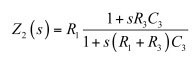 (32)
(32)
要取消分母,并让这个阻抗大小接近无穷大,您必须解得:
![]() (33)
(33)
从而
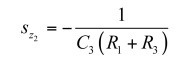 (34)
(34)
因此,起媒介作用的type 3传递函数是:
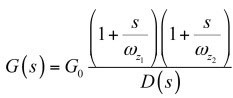 (35)
(35)
其中:
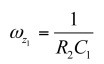 (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
作者:Christophe Basso,安森美半导体公司
本文来源于电子技术设计。
