技术解析：在FPGA上利用Python 实现定点平方根
品慧电子讯作为可编程的逻辑器件，FPGA便于调试、修改、功耗低，能够完成大量算法。在处理图像和信号时平方根运算被广泛使用。在FPGA上利用VHDL和Verilog等编程语言进行硬件设计，存在仿真和校验效率低、算法复杂等问题。而Python以其简单、功能强大的特点在此次设计中起到关键作用。 一、平方根实现 平方根的FPGA实现方法很多，有的算法为了减少片上资源的使用，逻辑实现上尽量避免使用乘法，比如CORDIC,逐位计算，non-restoring 等，现在FPGA上通常都有硬件乘法器，可采用迭代法和泰勒级数展开，本文采用泰勒级数展开的方法，级数采用5级，系数采用3.15的定点表示形式，小数部分15位，整数部分2位为了保证后续计算结果不溢出，整个位宽为18位，计算公式如式(1)所示：
对于输入x 位于(65 536,0]之间，由于数的范围较大，通常进行归一化处理，采用的方法通过左移运算去掉二进制定点数的所有前导零，将输入的数转换为定点小数[0.5,1)之间，在完成平方根运算之后，然后根据前导零个数的奇、偶性不同分别进行去归一化处理，原理如式(2)所示，将输入数y 分为sx,s=2n,n 即为y 的二进制前导零的个数。
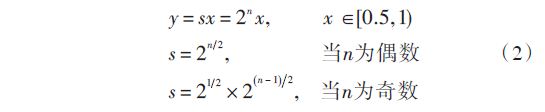整个过程的设计模块如图1所示。
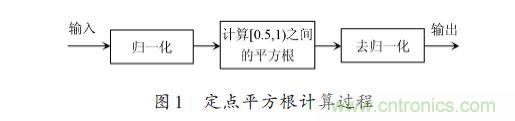二、定点数表示 通常在FPGA 上的运算可以采用定点和浮点两种方式来实现，定点运算和浮点运算相比尽管数表示的范围较小，设计较为复杂，但是速度较快，占用FPGA资源较小，本设计采用定点来完成。平方根的输入为非负数，包括符号位为定点32位输入，其中高16位为整数部分，低15位为小数部分，可以直接计算的平方根范围为(65 536,0],结果采用32位输出，最高位为符号位，接着的高8位为整数部分，低23位为小数部分。三、实验环境 采用MyHDL 0.8,采用GTKWAVE 查看仿真波形，FPGA 器件采用Altera公司CycloneⅡ 2C35F672C6,编译综合采用Quartus 12.1sp1 webpack.四、Python软硬件协同设计 基于Python 的软硬件协同设计的过程如图2 所示，由于本设计最终要在硬件上实现，在设计时Python的硬件设计部分采用MyHDL 可综合子集，最后使用MyHDL的toVerilog()函数将MyHDL设计自动转换为相应的Verilog 代码，由于MyHDL 支持与Verilog 混合仿真，设计时的测试平台可以重用，仿真速度和设计效率大大提高。在完成基于Python软硬件设计并仿真正确之后，就可以回到进行传统的FPGA 设计流程，进行后续的下载，综合和测试工作。
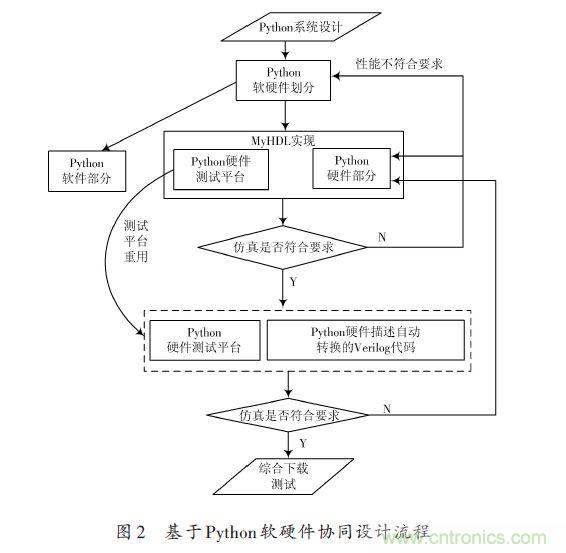12下一页> - 第一页：平方根算法实现的环境及过程；
- 第二页：平方根算法实现的测试结果
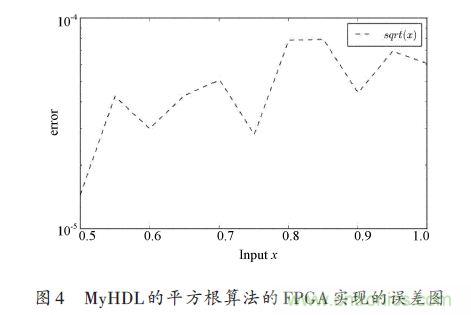
六、测试数据，精度及误差 由于整个过程采用Python设计，Python存在大量的软件包可以使用，平方根完成的测试数据结果如表1所示，采用基于Python 的绘图包matplotlib 绘制的当x 在[0.5,1.0]之间时的平方根误差如图4所示。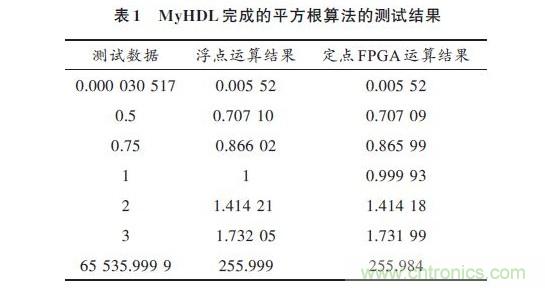
七、综合结果 在上面仿真校验符合设计要求后，将Python自动转换为Verilog描述，采用Quartus编译综合，并使用Model-sim仿真的波形如图5所示，与图3的Python环境下仿真波形相似，由此可见采用Python的软硬件协同设计方法能有效地进行FPGA 设计。综合后FPGA 资源使用情况：LE共1 506个，寄存器64个，嵌入式9位硬件乘法器10个。
结语：本文在FPGA 上利用Python的扩展包MyHDL完成了定点平方根算法，仿真校验和传统的设计方法仿真速度更快，效率更高，实现了将软件算法向硬件转换，完成软硬件系统协同设计。
相关阅读：
专家分析：为何数字电源转换被抛弃？
简单电路让数字电源控制器与模拟控制兼容
电源设计技巧十例：多相数字电源解决方案应对挑战<上一页12
- 第一页：平方根算法实现的环境及过程；
- 第二页：平方根算法实现的测试结果
