试分析软起动器对电机过载保护的控制方法(下)
7.2 动作值的测量和控制
将式(17)、(18)、(19)变换为
A=t(N0.02-1) (20)
A=t(N-1) (21)
A=t(N4-1) (22)
在实际运行中可每经过一个等间隔Δt进行一次累加,逐次计算A值,逐次与K值比较,直至达到设定值K值,求出延时时间tr。
以式(21)为例,设

对应式(20)和(22)可以采用同样方法进行计算和控制。
但是应用此方法计算有两个问题需要解决:
(1)设定N的阈值
通常在K的设定值范围,在N=1.05的条件下,计算值tr很可能小于1h,不能满足软起动器要求。为了防止在1.05Ir及以下的误脱扣,需设定阈值,如设定Nd=1.15,当N≤Nd时可仍按基本数学模型控制和计算。
(2)阈值上下数学模型的转换
如在N>Nd时,按式(20)~(22)的数学模型进行计算和控制。
现举例说明如下
保护特性取式(21),设定K=13.5
根据式(12)计算T值,取k2=1.15
T=13.5/1.152=10.2
在N≤Nd时按前面第4节所述方法进行计算和控制。
在N>Nd时按式(21)的数学模型进行计算,如果在尚未达到动作值时电流又下降使N≤Nd,并且当前A值为Ay。则此后需按基本数学模型累加计算A值:
式中初始值Ay为原数学模型下保留的A值。以下按前面第4节所述方法进行计算和控制。
如果此后又回复N>Nd条件,应重新按式(21)的数学模型计算和控制。在反复转换数学模型时不需改变K值和当前的A值。
保护特性取式(22),设定K=1200
根据式(12)计算T值,取k2=1.15
T=1200/1.152=907.4
在N≤Nd时按前面第4节所述方法进行计算和控制。
在N>Nd时按式(22)的数学模型进行计算,如果在尚未达到动作值电流又下降至N≤Nd,并且当前A值为Ay。则需按式(24)计算A值。
如果此后又回复N>Nd条件,应重新按式(22)的数学模型计算和控制。在反复转换数学模型时不需改变K值和当前A值。
7.3 误差分析
对式(16)微分
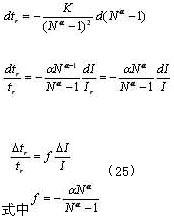
式(19)、(20)和(21)三种数学模型时间相对误差与电流相对误差之间的传递系数计算值见表3。
表3 三种数学模型时间相对误差与电流相对误差之间的传递系数计算值

由表3中可见,当α=0.02和α=1时在Nr≥1.5的情况下,要满足延时时间的误差不超过±10%的要求并不困难;但是在α=4时,因特性曲线斜率值大,要达到同样的指标是有一定难度的,即使电流测量误差为±2%,再考虑K的控制误差和数值化整等因素,延时时间的误差也可能大于±10%。
8 结束语
本文提出的一套利用数值积分法解决反时限保护特性的实时测量和控制方法,既可比较合理、方便的**多种保护特性,又可较好的解决负载不断变化情况下的热记忆问题,还有助于提高长延时控制单元的抗干扰能力。
由于在实时控制中,微处理器在很短时间内无法完成一些函数的复杂数学运算,本文中的一些计算公式和参数在工程计算中需要进行了变换和处理,在CMC系列软起动器中得到了应用,通过实际运行达到了理想的效果。
