信号传输理论的概念及噪声传导和反射(1)
噪声传导藉由导体传导性和空间传导性产生。在解释导体传导性的本质时，可能会运用传输理论概念。为便于理解以下内容，我们将用一种简化的方法解释EMC中用到的传输理论概念。
在传输理论中，导体被视为传输线路，电能在传输线上以波的形式传导，并在末端发生反射。无论传导的能量是信号还是噪声，都同样是以波的形式传导的。因此，本章节首先针对信号先解释了传输理论的概念，进而讲述噪声的传导。
数字信号对脉冲波形的影响
(1) 反射导致谐振
当数字信号与10cm或更长的导线相连时，可能导致如图1所示的振铃现象。如上一章节所述，由于线路中存在电感和静电容量，这可以解释为谐 振。但是，根据传输理论，由于导线两端信号波发生如图2所示的反射，也可以认为导线本身作为一种谐振器，让特定频率成分变得非常明显。这样一来， 传输理论就从电波传导和反射的角度解释了这种现象。
运用传输理论可以预测，在振铃的振荡频率处以及更高频率范围内会出现频谱（图中460MHz和860MHz）增加的现象（如图1(c)所示）。
(2) 反射会干扰信号波形的传输
如果发生反射或谐振，脉冲波形无法正确传输。为正确传输信号波形，需要抑制导线两端的反射。利用传输理论，可以提出一种抑制反射的设计，并预测反射导致的波形变化。
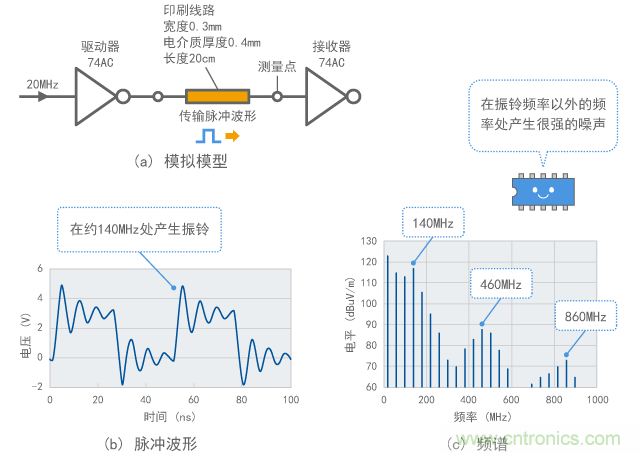
图1 数字信号中振铃的示例
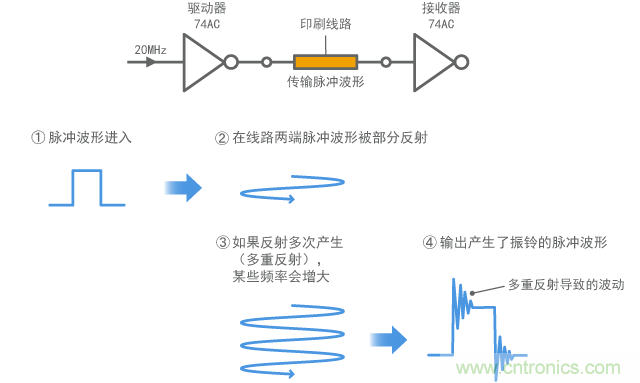
图2 数字信号中产生振铃的机制
特性阻抗和反射
(1) 阻抗匹配
为抑制导线两端的反射，需要执行“阻抗匹配”。“匹配”一词指的是匹配导线的“特性阻抗”与连接至导线端的电路的“阻抗”。
(2) 特性阻抗
如图3中信号线路所示传导电波的导体被称为信号线路。通过传输线路传输电时，电力和电流之间的比率恒定。这一比率就称为特性阻抗。特性阻抗由每单位导线长度的电感和静电容量决定（如图3所示），是无损传输线路的纯电阻。大家提到同轴电缆时说50Ω或75Ω，就是指的特性阻抗。如果本课程中没有另作规定，我们则认为传输线路处于理想状态而且没有任何电阻损耗，以便简化理论和表述。这也适用于后面的章节。（如果存在损耗，特性阻抗就不是纯电阻，会使整个概念更加复杂。）
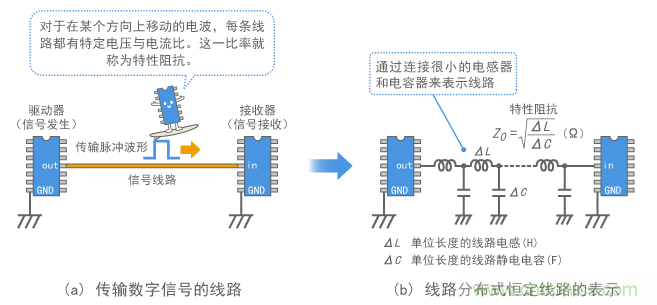图3 信号线的分布式恒定线路模型(3) 负载、终端、终端匹配
如图4(b)所示，当连接至导线端（以下称为终端）的电路阻抗（以下称为负载）与特性阻抗相等时，全部电能将被传输到负载，而不会发生任何反射。信号波形也被正确传输。在这种情况下，可以说此导线的终端是终端匹配的。
(4) 匹配能传输全部能量
如果导线端连接至另一个电路而不是负载，则电路的输入阻抗会被视为负载阻抗，以考虑阻抗匹配。当电路的输入阻抗与传输线的特性阻抗相同时，可以传输全部能量。在这种情况下，可以说这两个电路相互匹配。
在噪声抑制中，能量传输并不总是好事。在噪声传输路径与噪声源或天线相互连接之处，形成较差的阻抗匹配更有利，这样才不会传输噪声能量。
(5) 反射波
如果负载阻抗不同于特性阻抗，信号能量会被部分反射，并通过传输线路逆流，如图4(c)所示。这种波被称为“反射波”，反射的大小以“反射系数”表示。如果发生反射，则会在终端处观察到加入了输入波和反射波的波形。
(6) 数字信号中包含的反射波
图5提供了数字信号与传输线路和负载相连时所产生波形的一个示例。如图5(a)所示，一根28cm长的导线（特性阻抗为50Ω）传输33MHz时钟脉冲发生器信号。
图5(b)给出了所连接负载具有与导线特性阻抗相同阻抗时的情形。脉冲波形被正确传输。（因为时钟脉冲发生器的输出电阻大，上升时间约为2ns。）
(7) 通过增加行波和反射波形成数字信号
图5(c)给出了连接数字IC时的情形。信号振幅增加，同时可以观察到一些过冲和下冲。观察到的波形是由终端处产生的反射波和原信号右向行 波相重叠产生的。这就意味着终端处产生了具有与原信号相同迹象的反射波（图4(c)），因此信号振幅看起来比原信号更大（图5(b)）。
与此相反，还存在另一种情形: 反射波的迹象与原信号相对，使信号振幅比原信号小。
表示反射波的这种迹象（更准确的说是相位）和大小的系数是反射系数。<上一页1234567下一页>
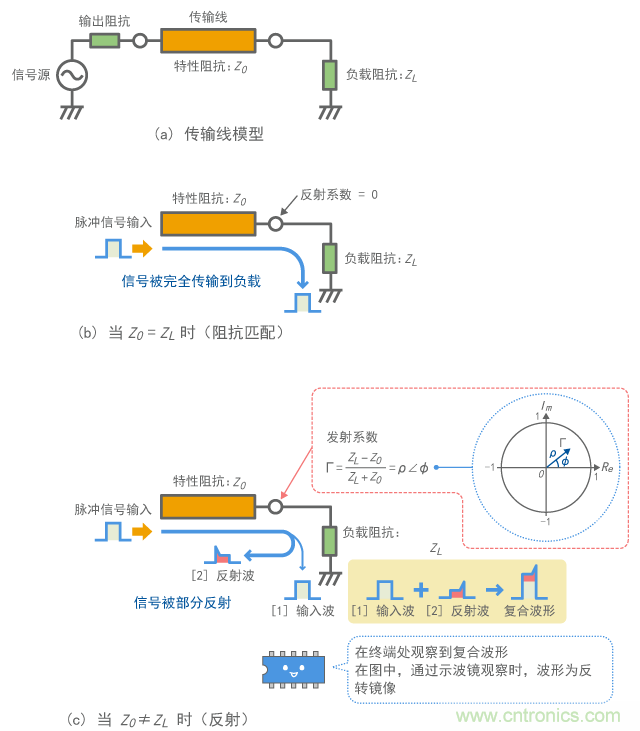图4 信号反射和匹配
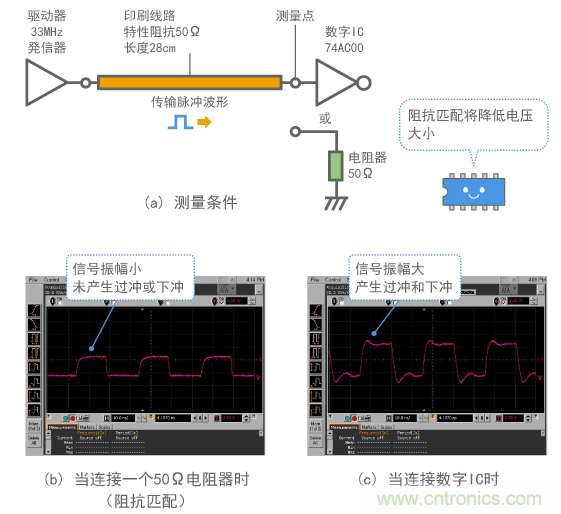图5 发生反射时数字信号波形的示例(8) 反射系数是矢量
反射系数Γ是一个矢量，其大小为ρ，相位角度为Φ，可在复杂平面上标绘在半径为1的圆内（如图4(c)）。因此，ρ的取值范围为0到1。
ρ=1表示全反射，而ρ=0表示无反射。通常而言，该值随频率而变化。
随着特性阻抗和负载阻抗之差变大，反射会越来越强，因此，ρ值增加（更接近圆的边缘）。如果是完全反射，ρ等于1，标注在圆周上。
(9) 反射系数位于圆心意味着“匹配中”
在未发生反射时（匹配中时），反射系数被标绘在圆心处。按照前述方法通过圆内的位置来表示反射系数，会有助于从直观上理解反射的状态。史密斯圆图就采用了这种方法。
另一方面，也可以根据特征阻抗和反射系数计算负载阻抗。
反射系数的概念也会用于后面讲述的S参数。S参数是非常重要的概念，因为它们广泛用于高频波（并不局限于噪声）的电子测量。
数字电路阻抗匹配
(1) 数字信号特性阻抗
数字信号所使用信号线的特征阻抗有多大？如图6所示，在以电源层和接地层为内层的4层电路板的表面有一根信号线，此信号线可以作为微带线（以下称为MSL）来处理，其中信号线的特性阻抗约为50Ω到150Ω。（如果有电源线，特性阻抗值可能更小。）
(2) 很多数字电路都未实现阻抗匹配
与此相反，数字IC的输入阻抗通常一个几pF的电容，在频率为100MHz及以下时，会变成100Ω以上的高阻抗。因此，如图7所示，数字电路的设计基本上会产生非常高的反射，从而导致在接收器处反射大部分信号能。
此外，数字IC驱动器侧的输出阻抗也会变化。因此，阻抗匹配并非总是在驱动器侧完成，而且也可能导致反射。所以，数字信号一般会在信号线两端造成反射（如图2所示），而且会在造成多重反射一定程度时被传输。
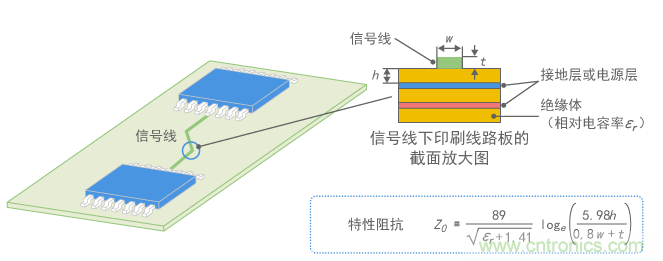图6 信号线的特性阻抗
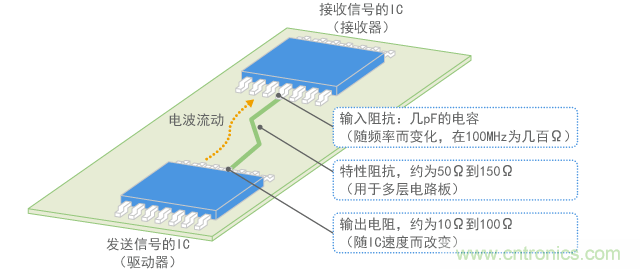图7 数字信号线的阻抗匹配状态(3) 驻波指示匹配状态
尽管为了便于解释在图4中分别描述了输入波和反射波，但在正常测量中很难单独观察这两种波形（因为示波镜只会显示复合波形）。因此，可以按照后面的讲述，通过观察驻波来确定反射状态。
如果因驱动器侧和接收器侧的反射而产生多重反射，传输线会形成一种谐振器，使某个特定的频率变得特别明显。从正确传输数字信号波形（即“信号完整性”）的 角度而言，传输线产生的谐振并不可取，因为它会导致振铃。此外，从EMC的角度来看，这也是不可取的，因为它会在谐振频率处增加噪声。为抑制传输线产生的 谐振，导线的两端或者一端应该靠近匹配状态，以便吸收反射。
驻波
(1) 电压和电流随测量点变化
在一定频率处测量信号线上的噪声时，如果终端处产生反射，就会观察到如图8所示的驻波。在这种现象中，您会发现由于“入射波”（原信号）和反射波之间发生干扰，不同位置的信号长度会有所不同。这种驻波是传输线路复杂状况的根本原因，这将在后面进行描述。
如图9所示，驻波较强处称为“波腹”，而较弱处称为“波节”。波腹和波节的位置随频率而有所不同。就其本质而言，电压的波腹位置会成为电流的波节，而电压的波节位置会成为电流的波腹。
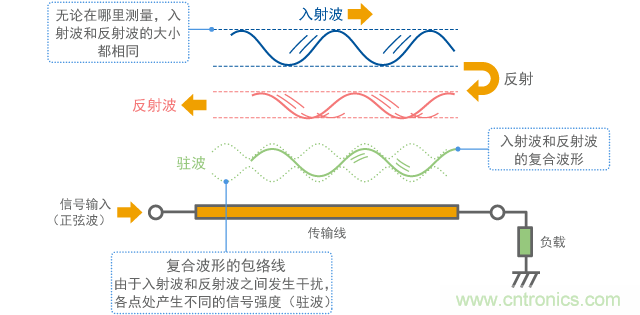
图8 驻波
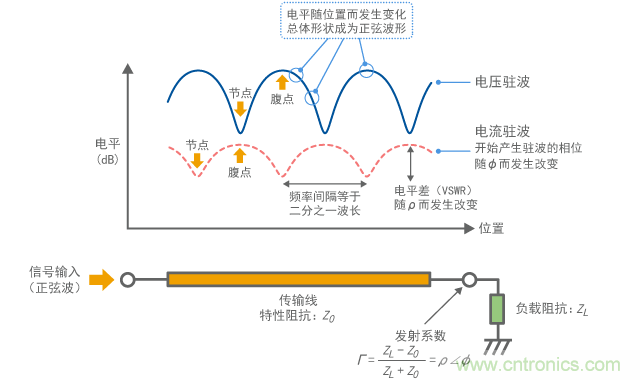
图9 电压驻波和电流驻波
(2) 观察数字信号中包含的驻波图10到12提供了观察如图5所示数字信号波形的驻波的示例。在此，28cm长的信号线连接至33MHz时钟脉冲信号，以 便观察信号线周围的磁场和电场。磁场和电场分别对应电流和电压。观察的频率为490MHz（33MHz时钟脉冲频率的第15次谐波），测量间隔为5mm。
在各图中，(a)的信号线右端有一个50Ω电阻器，以便近似得到阻抗匹配的状态，而(b)中有数字IC输入终端。
(3) 电流驻波
图11给出了磁场的测量结果。尽管(a)（有阻抗匹配的终端）显示传输线上具有恒定的磁场，(b)却指出了不同位置处的强磁场（红色）和弱磁场（蓝色）。这就意味着红色部分具有较大的电流。这被称为驻波，其中较高反射系数ρ会导致最大值和最小值之差更大。
(4) 电压驻波
图12给出了电场的测量结果。与电流的情形一样，(b)中使用数字IC作为负载，指示了不同位置处的变化。对比图11和图12会发现，就产生较强噪声的位置而言，电压和电流的情况正好相反（如图9所示）。
如果产生了驻波，噪声电平可能会随不同位置而变化。因此，不能只通过某个位置测得的单个结果确定噪声强度。<上一页1234567下一页>
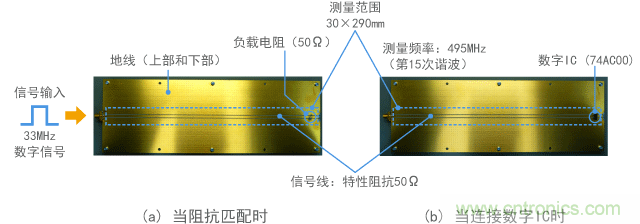
图10 驻波的测量范围
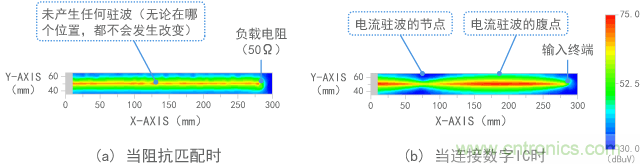
图11 磁场（电流）的测量结果
图12 电场（电压）的测量结果
(5) VSWR
图12所示电压驻波的波腹（最高点）和波节（最低点）之比率称为VSWR（电压驻波比率），它是表示反射程度的指数。对于电压和电流而 言，VSWR趋于一致。如果没有驻波，VSWR为1。反射越强，VSWR的值越大。根据图中的测量结果，(b)中观察到了驻波，指示VSWR约为4。
(6) 驻波周期为二分之一波长
驻波一个周期（波节到波节）的长度为频率的二分之一波长。因为后面将要讲述的阻抗变化和传输线谐振是以此驻波为基础的，它们可能在使传输线长度为二分之一波长整数倍的每个频率处反复出现。
图11和图12(b)的示例表明驻波的一个周期约为200mm，这说明传输线上的一个波长为400mm。在真空条件下测量的490MHz 处的波长约为600mm，这表明在该传输线上波长缩短至三分之二。这个缩短比率会随着基板的相对介电常数而变化，介电常数越大，波长就会越短（这意味着电 波在基板上减缓）。阻抗因传输线路而变化
(1) 什么让阻抗出现变化？
从传输线的角度而言，信号线的另一个重要特性在于通过信号线的负载阻抗与阻抗本身完全不同。
例如，在连接至图1所示20cm长信号线的数字IC的输出终端，阻抗是多少？为找出答案，连接一个电阻器（10Ω: 紫色，1000Ω: 蓝色）、一个电容器（5pF: 绿色）和一个电感器（50nH: 红色）作为负载（如图13所示），并测量阻抗。如果数字IC如图1所示连接到终端端口，阻抗可能接近于电容器（5pF）的阻抗。
图14指出了计算模型。(a)表示不考虑信号线的情形，而(b)显示通过传输线路测量的情形。此外，(c)给出了按照第3章的章节3-2所述以线路模拟单级LC电路的情形，仅供您参考。
计算结果如图15所示。情形(a)（未考虑信号线）指出不考虑电阻器情况下的恒定值。电感器和电容器分别显示出与频率成正比/反比的阻抗。
(2) 阻抗因传输线路而振荡
相反，情形(b)（考虑传输线路）在10MHz频率以上比(a)中的差异大，在100MHz频率以上表现出复杂的波动情况。仔细观察就会发现，阻抗似乎以信号线的特性阻抗（该示例中为123Ω）为中心，在其附近振荡。如上所述，纵观整条传输线路，阻抗在高频范围内似乎存在显著差异。尽管图15仅显示了阻抗的振幅，但其相位也发生了变化。因此，根据不同频率，电 感器可能类似于电容器，而电容器可能类似于电感器。（在某些情况下，利用这样的特性，传输线路可以用作阻抗变换器或者用于阻抗匹配。）
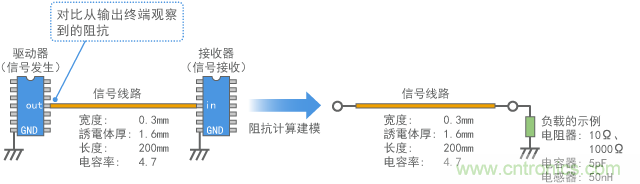
图13 从数字电路输出终端观察到的阻抗
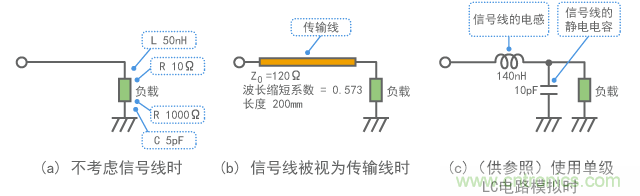
图14 计算模型
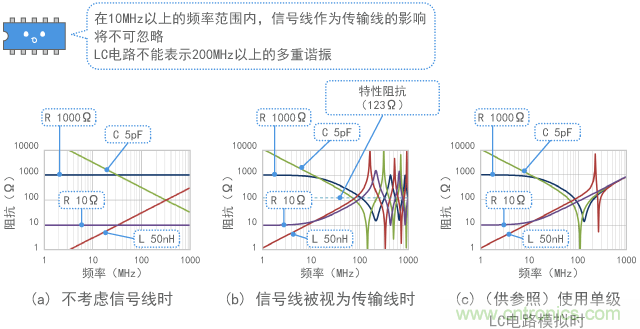
图15 阻抗对比
(3) 入射波和反射波之间的相位差导致阻抗变化
在图15(b)的计算结果中，连接5pF电容器的情形（绿线）表现出的特征相对接近使用数字电路作为负载的情形。计算结果表明100MHz 到200MHz之间存在局部最大阻抗。在200MHz以上频率范围内，阻抗交替出现局部最高点和局部最低点，呈现出周期变化。阻抗的局部最低点和下一个局 部最低点之间的频率间隔等于使导线长度为二分之一波长的频率。如上所述，传输线的态势与导线长度和波长之间的关系有着密切的关联。
(4) 注意导致局部最小阻抗的频率处的噪声
因为导致局部最小阻抗的频率容许很大的电流，所以需要特别注意EMC措施。脉冲波形可能导致振铃或者可能发射很强的噪声。
