为同步整流选择最优化的MOSFET

中心议题：

• 同步整流基础知识
• 优化同步整流MOSFET

解决方案：

• 确定优化MOSFET的负载电流
• 借助四象限SR器件优化表选择MOSFET

1. 引言

电源转换器的封装密度日益提高和节能标准越来越严格，要求不断提高电源级的能效。隔离式电源转换器的次级整流产生的严重的二极管正向损耗是主要的损耗，因此，只有利用同步整流（SR）才可能达到这些标准要求的能效水平。用MOSFET替代二极管引发了新的挑战——优化系统能效和控制电压过冲。本应用笔记介绍了通过利用英飞凌OptiMOS™3解决方案的优化表（适用于30 V、40 V、60 V、75 V、80 V、100 V、120 V和150 V等应用）帮助选择最佳MOSFET的方法。

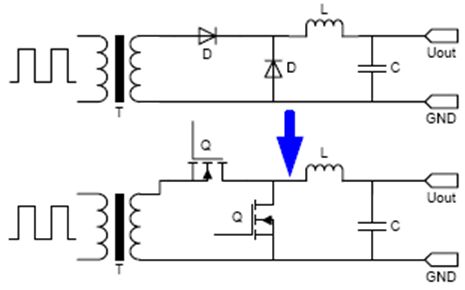
图1. 二极管整流与同步整流之比较

2. 同步整流基础知识

要选择最优的MOSFET来实现同步整流，必须充分理解MOSFET的功耗产生机制。首先，必须区分开随负载而变化的导通损耗与基本保持不变的开关损耗。导通损耗取决于MOSFET的RDS(on)和内部体二极管的正向电压VSD。随着输出电流的提高，导通损耗（RDS(on)损耗）也会相应地增加。为确保两个SR MOSFET之间互锁，以避免出现直通电流，必须实现一定的死区时间。因此，在开启一次侧之前，必须关断相应的MOSFET。由于该MOSFET正在导通全部续流电流，因此，这些电流将不得不从MOSFET沟道转而流向内部的体二极管，并由此产生额外的体二极管损耗。体二极管的导通时间很短，仅为50 ns至100 ns左右，因而，当输出电压比体二极管的正向电压高得多时，这些损耗可以忽略不计。

取决于电源转换器的开关频率和输出负载，开关损耗对MOSFET的总功耗有很大影响。MOSFET开启时，必须对栅极进行充电，以产生栅极电荷Qg。MOSFET关断时，则必须将栅极中的电荷放电至源极，这就意味着Qg将消散在栅极电阻和栅极驱动器中。对于特定MOSFET技术，栅极驱动损耗会随着RDS(on)的降低而增加，因为硅片越大Qg就越多。

在总开关损耗中占很大比例的另一种损耗与MOSFET的输出电容Coss和反向恢复电荷Qrr有关。MOSFET关断时，必须将Qrr移走，并且必须将输出电容充电至次级变压器电压。这个过程会导致反向电流峰值，该电流将耦合到交换环路的电感中。所以，这些电量将被转移至MOSFET的输出电容，加上之前存储的电量，将由此产生电压尖峰。这些电量将触发LC振荡电路。LC振荡电路的性能取决于印刷电路板的感应系数和MOSFET的输出电容Coss。LC电路的寄生串联电阻将减弱振荡。由于这种在关断过程中产生的感应电量直接取决于MOSFET Coss（相应地，当输出电容被充电至次级变压器电压时，则为输出电荷Qoss），因此，总Coss决定了容性关断损耗。对于栅极电荷也是如此，Qoss会随着RDS(on)的降低而增加。因此，总是能找到可以实现最高效率的导通损耗与开关损耗之间的平衡点。

大致上，对于OptiMOS™3产品而言，Qrr可以忽略不计，因为其对总功耗的影响微乎其微。在这种情况下，Qrr仅被视为MOSFET体二极管的反向恢复电荷，而数据手册中的Qrr则是按照JEDEC标准测得的，因此，除体二极管Qrr之外，还包含MOSFET的部分输出电荷。此外，其他因素也会导致应用中的实际Qrr值低于数据手册所提供的Qrr值。数据手册中的值是在对体二极管施以允许的最高MOSFET漏极电流、体二极管导通时间长达500 μs并且di/dt值固定为100A/μs的条件下测得的。在实际应用中，通常电流仅为最高漏极电流的三分之一左右甚至更低，体二极管导通时间在20ns至100ns范围内，并且di/dt可能高达800A/μs。
123下一页> 关键字：同步整流 电源转换器 MOSFET SR  本文链接：http://www.cntronics.com/public/art/artinfo/id/80013709
3. 优化同步整流MOSFET

要优化SR MOSFET的效率，必须找到开关损耗与导通损耗之间的最佳平衡点。在轻负载条件下，RDS(on)导通损耗占总功耗的比例极低。在这种情况下，在整个负载范围内基本保持不变的开关损耗是主要损耗。但是，当输出电流较高时，导通损耗则成为最主要的损耗，其占总功耗的比例也最高，请参见图2。

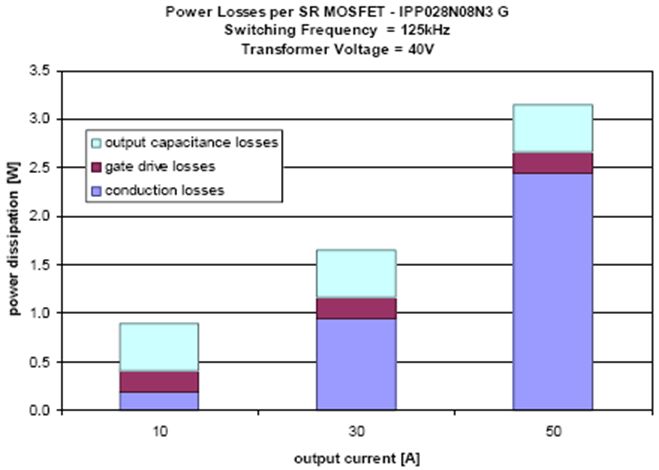
图2. 功耗构成与输出电流的关系

在选择最适当的MOSFET时，必须特别注意RDS(on) 的取值范围，如图3所示。当RDS(on)超出最优值时，总功耗将随RDS(on)的提高而线性增加。但当RDS(on) 降至低于最优值时，总功耗也会因输出电容的快速增加而急剧上升。此外，在图3中可以看出，可实现最低功耗的RDS(on)值范围相当宽。在本例中，当RDS(on)在1毫欧姆至3毫欧姆范围内时，总功耗始终大致相同。但是，在此范围之外，RDS(on)仅下降0.5毫欧姆，便会令总功耗提高一倍，从而严重降低电源转换器的效率。

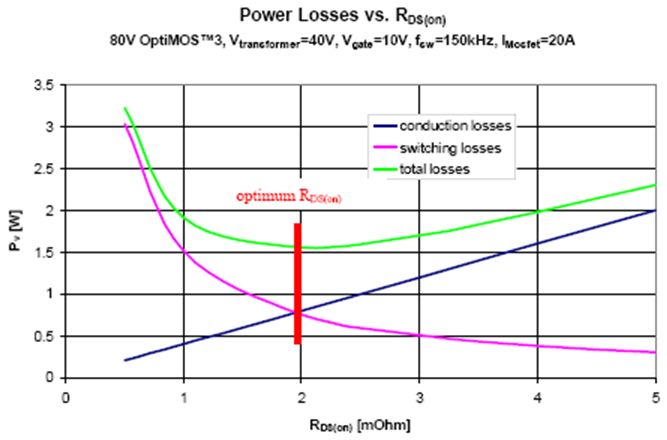
图3. 功耗与RDS(on)值的关系

对于优化SR，另一个重要的问题是正确选择MOSFET封装。只要将TO-220封装替换为SuperSO8封装即可实现效率提升。这是因为，SuperSO8封装的电阻占总RDS(on)的比例更低。在降低RDS(on)的同时，保持输出电容不变，能够降低FOMQoss。FOMQoss是特定MOSFET解决方案的性能指标（FOMQoss= RDS(on) * Qoss）。因此，降低FOMQoss可以降低开关损耗，从而提高系统能效。
<上一页123下一页> 关键字：同步整流 电源转换器 MOSFET SR  本文链接：http://www.cntronics.com/public/art/artinfo/id/80013709?page=2
4. 应当按何种负载电流优化MOSFET？

要在整个负载范围内实现均衡的效率，必须借助四象限SR器件优化表对MOSFET电流做出合理的选择。采用满负载优化，可以在输出电流较高时实现良好的效率。但是，当负载较低时，这种方法会大大降低效率，并且所需并联MOSFET的数量将多得不能接受。因此，必须找到最优MOSFET电流，以在整个输出电流范围内实现相对恒定的效率值。

为阐明这个问题，图4显示了不同优化方法得到的效率。图中所示效率曲线为，当变压器电压为40V、栅极驱动电压为10V、开关频率为100kHz时计算得到的12V同步整流级的效率。在75V优化表中选择 IPP034NE7N3，按10 A MOSFET电流进行设计，所得到的优化方案仅需一个MOSFET。如图4所示，这种优化方案能够在低电流时实现很高的效率，而在高电流时效率却极低。按50 A进行优化设计，所得到的最佳方案则需要5个MOSFET。采用这种优化方案，低电流时的效率将低得不能接受，但在满负载时可以达到最高效率。因此，对该设置而言，最佳优化方案是采用两个并联的MOSFET，从而获得整体均衡的效率。

通常，按最高输出功率的20%至30%对MOSFET进行优化，可以获得均衡的总体效率。对于强调轻负载效率的系统，可以按最高电流的10%至20%的低电流进行优化；而对于高负载设计，则适于按最高电流的60%进行优化。应当避免按100%输出负载进行优化，因为这会严重降低系统的低负载效率，并大大增加所需并联的MOSFET数量。

图4. 不同优化方法实现的效率不尽相同

5. 借助四象限SR器件优化表选择MOSFET

为了帮助开发人员更轻松地为SR应用选择最优MOSFET，下面介绍一个四象限SR器件优化表。借助这个优化表，可以根据三个应用参数找到最适合的器件：次级变压器电压、开关频率和RMS MOSFET电流。为便于理解，图5给出了一个实际的例子。

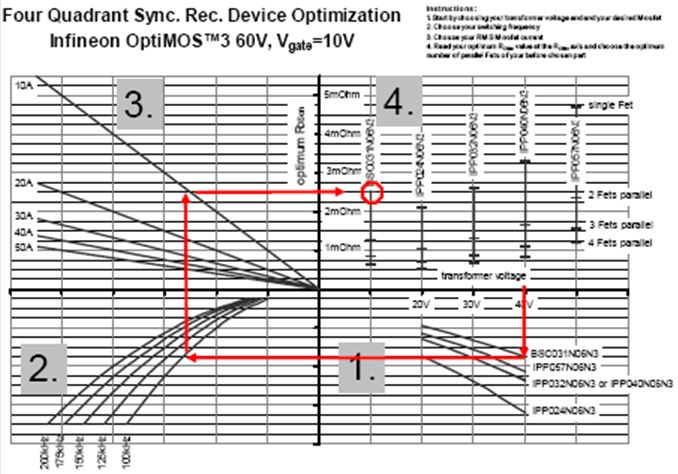
图5. 四象限SR器件优化表

使用优化表时，首先从次级变压器电压开始。在所用电压值位置，画一条垂直的直线。在两条线相交处可以选出特定的MOSFET。通过一条水平的直线和一条垂直的直线，便可选择开关频率和MOSFET电流。如前面所讨论，按最好从满负载的20%至30%的电流值开始进行选择。此时，可以在正Y轴上读取最优RDS(on)值。在第四个象限中，显示了并联MOSFET的最佳数量。在第四个象限中，必须选择之前在第一个象限中选定的MOSFET型号。然后，按同样的参数（变压器电压、开关频率和电流RMS）对另一个型号的MOSFET重复执行这个选择过程。比较两次选择所得到的最优RDS(on)值，最优RDS(on)值越低的MOSFET所产生的功耗也越低，因而是更加高效的解决方案。

这个MOSFET选择方法，是在假定应用具备最优开关性能的条件下计算得到的。如果发生了诸如动态开启或雪崩等二阶效应，那么这个优化表可能不准确。此外，硬开关转换器拓扑可实现最佳结果。任何谐振软开关拓扑均可能导致失配，因为可以回收利用开关过程产生的部分电量。在这种情况下，实际最优RDS(on) 值将低于计算得到的值。请注意，一次侧采用准谐振拓扑（例如相移ZVS全桥）也可使二次侧的同步整流实现硬开关性能，从而也可以利用这种设计优化表来进行优化。

从这种优化表得到的所有结果，均以理想的MOSFET性能为前提。根据经验，实际应用的结果与按理想状况计算得到的结果有所不同。因此，利用这种优化表得到的结果应作为最优器件选择的参考，以防止MOSFET性能不足或过高。如果利用这种优化表得到的结果是在两个不同的并联MOSFET数量之间，那么，数量较低的方案是适于低负载的优化方案，而数量较高的方案则是更适于高功率的优化方案。此外，任何与同步整流级并联的缓冲网络均会影响器件的选择，因此，在设计时也必须予以考虑。

要在整个负载范围内实现总体优化，仅一次计算是不够的。除按特定负载值（电流值）计算最优MOSFET之外，还需要按不同负载电流在这个四象限优化表上进行多次计算，以扩大优化范围。同时，还要根据实际应用要求，调整所得结果。