RF系统设计中信噪比测量参考点的选择
解决方案:
- 电路元件模型
- Pr/N0的系统模型
- Eb/N0的位置和模型
在无线产品的接收系统中,哪里是建立SNR的正确参考点?一般来说,系统设计工程师、天线设计工程师和系统中发射器一侧的设计工程师常常有不同的选择。而实际上任何位置都可作为参考点。本文通过深入研究参考点选择过程出现的各种问题,给出了克服由系统噪声测量参考点的不确定所引起的误差的解决方案。
在数字通信系统中,接收信噪功率谱密度比(Pr/N0)、接收位能量与噪声功率谱密度比(Eb/N0),以及其它类似的信噪比(SNR)常常被不太准确地定义在接收电路的输入点处。这种不精确性来自于一些常见的不确定性,包括应该在哪里定义和测量这些SNR,以及对于接收系统中的(Eb/N0而言,恰当而准确的参考点应该位于何处等问题。
这种不确定性必然会导致误差,它与本地SNR测量对应于一个系统SNR模型这一错误假设(实际情况并不总是如此)混杂在一起。此外,接收电路设计工程师常常在接收电路内部为SNR(以及系统温度)模型选择一个物理位置,它不同于系统设计工程师通常用作参考的位置。
为了减小潜在误差,设计工程师需要明确地区分测量和模型,而且必须完整地理解对这些接收电路SNR参数的模拟是如何发展演变的。此外,通过认识通信系统中各方面的差异(应该在哪里测量SNR和系统温度),可以避免在系统分析中犯错误。
简单地说,一个数字通信接收电路系统(图1)包括一副接收天线,一条损耗线,一个主要由放大器、相关器或匹配滤波器和采样器组成的接收电路,以及一个执行离散判决的检测器功能块。为简化起见,接收电路功能块中的下变频和均衡等功能没有显示出来,整个接收电路功能块将被当作单个电路元件来看待。假设损坏接收信号的热噪声具有平坦的功率谱密度,其幅度为N0 = kT (W/Hz),其中k为玻耳兹曼常数,T为以开尔文为单位的温度值。

图1 数字通信接收电路系统
电路元件模型
有效噪声温度的概念是一个简单的模型,它允许设计工程师将电路元件的内部噪声表示为理想电路的噪声温度输入源。图2a是将这一概念应用于放大器和衰减器的情况,并总结了两个关系方程:
方程1: TR=(F-1)290 Kelvin
方程2: TL=(L-1)290 Kelvin
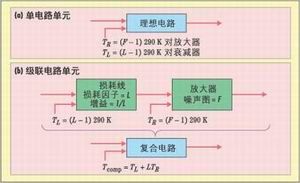
图2
上列方程中,TR和TL分别为放大器(接收电路)和衰减器(损耗线)的有效温度,F和L分别代表噪声谱和损耗因子。图2b是应用于一对级联电路元件(一条损耗线加上一个放大器)的模型,其中损耗线的增益可表示为1/L。
因此,复合噪声温度Tcomp可表示为:
方程3: Tcomp=TL + LTR
测量点
在接收电路中的某处进行SNR测量时,T代表该处的本地噪声温度(Tlocal)。如图3所示,Tlocal(其效果可在选择的某个观察点或参考点进行测量)代表源噪声功率。负载的影响忽略不计,因为计算SNR时它将被抵消。
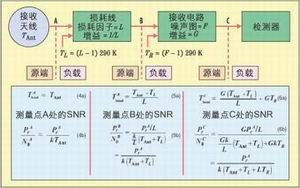
图3
测量位置
图3显示在接收系统中的A、B、C处对Tlocal和Pr/N0进行三次测量,参数中的上标A、B、C表示测量分别是在这些不同位置点进行的。对于每一个点,存在以下关系:
A点有方程4a和4b所示关系。其中PrA为接收信号功率(由A点波形测得),N0A为噪声功率谱密度,来自对A点的测量,TAnt为天线温度(图3中的源噪声温度)。
注意,SNR测量通常包括三个步骤。第一步是对通信系统施加一个信息信号,并在接收天线的输出上测量接收到的波形功率,接收波形的功率与信噪之和的功率成正比。
第二步,滤除信号,只测量接收到的噪声功率。最后一步是从第一次测量的结果中减去噪声功率,计算得到信号功率与噪声功率之比,即SNR
对于B点有方程5a和5b所示关系,其中PrB为接收信号功率(来自对B点波形的测量),N0B为噪声功率谱密度,由对B点的测量得到。方程2中已给出损耗线的有效温度TL。注意由方程5a和图3可知,(1/L) *(TAnt + TL)为B点的源噪声温度。
对于C点有方程6a和6b所示关系,C点代表匹配滤波器的采样输出(该输出为一基带脉冲),PrC为接收信号功率(来自对C点的测量)。C点的噪声功率谱密度N0C可通过(在无信号时)直接在C点测量噪声功率N得到。这是因为对于单边带功率谱密度为N0 (W/Hz)的热噪声而言,匹配滤波器的输出噪声功率等于N0 W。由方程6a和图3可知,(G/L)*(TAnt + TL) + GTR代表C点的源噪声温度。接收电路功能块的放大系数(即功率增益)记为G,其有效温度TR已在方程1中给出。
方程4~6表明,从A点到B点再到C点,SNR呈下降趋势。在每个点测量SNR时,可以忽略测量点右边的所有电路,因为任何负载对SNR的分子和分母的影响肯定是相同的。
预检波点
图1中接收电路的解调/检测功能可分解为两个步骤。第一步,在每个符号持续期间,相关器或匹配滤波器恢复出一个表示数字符号的基带脉冲,然后进行采样。采样器的输出(C点),即预检波点,产生一个测试统计量,它包含接收符号和噪声两个分量。测试统计量的电压值与符号和噪声中的能量成正比,因而包含了SNR的基本度量信息。
第二步对该符号的离散意义做出判决(检测),其结果是一个信息位(用于二进制调制的数字位)。检测的精度是预检波SNR的函数。在数字接收系统中,预检波点是所有错误性能分析关注的重要位置。位误码概率PB是Eb/N0的函数,得出这个函数是检测器功能块的一个重要作用,采样中信号的能量越多(相对N0而言),误差性能就越好。
因此,关于Eb/N0的位置,简洁的答案就是将它定义在预检波点处。但是问题在于答案过于简单,因为它不能反映在规定这些SNR时通常使用的模型。此外还应该注意,Eb/N0被定义在尚无任何信息位之处。检测过程结束之后,才会出现信息位。或许Eb/N0更恰当的名称应该是每个有效位相对于N0的能量.
链路预算
规划链路预算时,系统Pr/N0常常表示为方程7(以图3中的A点为参考),其中EIRP为发射天线输出的有效全向辐射功率,Gr为接收天线增益,Ls为空间损耗,Lo预留给其它损耗。方程7中,TS表示系统的有效温度,且N0 = kTS。稍后我们将考察这个模型。
链路预算可给出接收系统中检测数据质量的一些信息。即方程7得到的Pr/N0值可用来描述系统的误差性能。为此,这里给出的Pr/N0必须与图3中C点(预检波点)的测量值相对应。虽然系统Pr/N0不必用C点的测量值来表示,但无论采用什么模型(参考点),一定会得到一个等价的值,仿佛Pr/N0是在C点测量得到的一样。
SNR的历史
在数字通信发展的早期,Pr/N0的测量直接在图3中的C点处进行,或者在接收天线的输出A点处进行,然后再考虑由损耗线和接收电路导致的SNR恶化,将其换算到预检波点。稍后,Eb/N0是通过方程8所示的关系直接进行计算,其中R为数据传输速率,单位为位/秒。
开始用接收的预检波SNR来描述通信系统后,人们很快就认识到除C点之外,可用的Pr/N0系统模型也将允许同一预检波SNR在接收天线输出(或接收系统中的任何参考点)处进行表述。
在教科书上,Pr/N0和Eb/N0常常表述在接收天线的输出点处。这可能容易使人混淆,因为人们将认为可以直接将接收天线输出点的简单测量结果作为系统SNR直接用于链路预算分析的准备工作,而这是不正确的。系统SNR或Pr/N0只能在预检波点这个位置直接测量,但可以在接收电路中的其它位置进行模拟。本文的后续部分将介绍测量和模拟之间的重要区别,以及如何不将二者混淆,避免系统误差。模型可以方便地描述一个系统,从而可用简单的方程来表示分析这个系统。但是,模型的参数一般无法测量。由于没有与系统交互的手段,模拟操作不能(象测量那样)修改底层的进程。
Pr/N0的系统模型
每当使用一个以内部某点为参考的预检波SNR来规定或描述系统时,T就用该点模拟的系统温度(TS)来表示。我们将把系统温度记为TSx,其中上标表示参考点为x。图4表明,TSx代表该点的系统温度(而不只是源温度)。对于图中所示的各点A''、B''和C'',TSx可表示为方程9,其中参数TSx模拟点x之后的复合电路的噪声温度,在系统中不同的参考点处TSx一般各不相同。
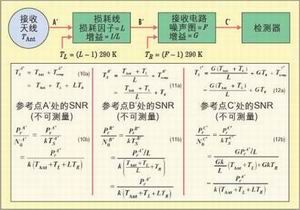
图4
图4给出了在三个不同点A''、B''和C''处模拟的预检波信噪比(现在可称为系统SNR)。这三个点代表了与图3中A、B和C点相同的物理位置。这种标记方式是为了强调现在不再在这些点上进行测量,而是以这些点为参考来模拟系统SNR。系统SNR只能在C''点(或图3中的C点)进行测量。对于点A''和B'',模拟的系统信噪比在物理上并不存在。这种标记方式也保证我们不会将图3中A点和B点的SNR测量值与图4中A''点和B''点的SNR模拟值(标号相似)等同起来。对于图4中的每个参考点,可以这样描述TS和Pr/N0的关系:
A''点:见方程10a和10b,其中TSA''是以A''点为参考的系统有效温度,由源噪声温度加上A''点之后的复合电路产生的噪声温度组成。TSA''''的深层意义是,它代表了一个模型,允许我们推测对图4中A''点处表现的整体系统噪声产生影响的所有的噪声温度。因此,我们可以推测表现在天线输出端的整体系统噪声。
B''点:见方程11a和11b,其中TSB''是以B''点为参考的系统有效温度。注意方程11b中的第三项表明了在B''点模拟时,系统有效温度是如何使得对整体系统噪声有影响的噪声温度表现在图4中的B''点的。
C''点:见方程12a和12b,其中TSC''是以C''点为参考的系统有效温度,假设TcompC'' = 0。
比较方程4~6中图3的关系与方程10~12中图4的关系可发现,前者随着从A点移动到C点,信噪比的下降反映了实际测量结果。另一方面,后者从A''点到C''点,系统Pr/N0比保持固定,反映了一个在接收系统中各个选择点产生系统(预检波)信噪比的模型。这种模拟的预检波SNR可表述在接收系统中的任何参考点处。在模型中,即使信号功率和系统温度在接收系统中的各个位置互不相同,系统中任何选定参考点处的系统Pr/N0比(其中N0 = kTS)仍然是相同的。
实际温度
我们将系统有效温度TS看作代表接收系统中所有噪声功率的参数。因此,对于一个给定的系统,是否仅有一个固定的TS值?有没有多个系统温度呢?答案是肯定的。系统有效温度是一个模型,代表系统中选定参考点的所有噪声功率。多数工程师习惯于只有一个参考点,因此对于给定的系统只按照一个固定的TS来考虑。需要注意的是,系统设计工程师、天线设计工程师和系统中发射器一侧的工作人员常常选择接收天线的输出点(图4中的A''点)作为TS和接收功率Pr的参考点。但接收电路设计工程师通常选择在接收电路的输入点(图4中的B''点)来描述TS和Pr。
假设天线和接收电路之间只通过一条损耗因子为L的损耗线进行连接,那么根据图4,TSA'' = LTSB''、 PrA'' = LPrB'',且A''点和B''点肯定具有相同的系统SNR。但是,对于方程7所描述的接收系统,Gr/TS是多少?不同的系统温度对它有什么影响?其表述是类似的:在A''点,它可表达为GrA''/TSA'',其中GrA''为接收天线的增益。在B''点,这个比率可等价地表示为方程13。
TS只有单一的值,但Pr或Gr的值不是单一的,它们各自受到电路环节中增益和损耗的影响,而且它们各自的值依赖于所选择的参考点。
Eb/N0的位置和模型
本文前面已简单给出结论,Eb/N0是在C点,即图3中的预检波点(或图4中的C''点)定义的。那么在模拟环境下,接收系统中的Eb/N0又应该以何处为参考点呢?前面讨论系统有效温度的模型时,可以从在接收系统中任意点表述的系统SNR得到同一个Eb/N0值。将图3中C点(方程6b)中的SNR与图4中C''点(方程12b)中的SNR进行比较可发现,C点测量的SNR值与C''点模拟的SNR值一致。这是因为,只有在这个预检波点,实际噪声温度TlocalC才等于系统的有效温度TSC''。对于其它位置,系统有效温度只代表一个简单的模型,其模拟值无法在参考点进行测量。在接收系统中用一个模型来规定SNR时,接收天线的输出点(图4中的A''点)是最常用作参考点的位置。
通过上述分析,我们回答了在一个接收系统中,哪里是建立或规定Eb/N0和其它类似SNR值的正确参考点的问题。假设已经有了一个精确的模型,答案是任何位置都可作为允许的参考点。不过,在接收电路规范的发展过程中,接收天线的输出点是这些SNR模型中最常使用的参考点。
