数字电容隔离器的磁场抗扰度
中心议题:
- 判断磁场方向的基本物理定则
- 介绍电容隔离器的结构
- 数字电容隔离器的磁场抗扰度分析
数字电容隔离器的应用环境通常包括一些大型电动马达、发电机以及其他产生强电磁场的设备。暴露在这些磁场中,可引起潜在的数据损坏问题,因为电势(EMF, 即这些磁场形成的电压)会干扰数据信号传输。由于存在这种潜在威胁,因此许多数字隔离器用户都要求隔离器具备高磁场抗扰度 (MFI)。许多数字隔离器技术都声称具有高 MFI,但电容隔离器却因其设计和内部结构拥有几乎无穷大的 MFI。本文将对其设计进行详细的介绍。
基本物理定则
诸如电动机的电源线等带电导体,其周围便是一个由流经它的电流形成的磁场。应用右手定则(请参见图 1),我们很容易便可以确定该磁场的方向。该定则的内容如下:用右手握住导体,然后拇指指向电流的方向,这时环绕导体的手指便指向磁场的方向。因此,磁通线的平面始终与电流垂直。
图 1 显示了 DC 电流的磁通密度 B。就 AC 电流而言,将右手定则用于两个方向,磁场和 AC 电流都随同一个频率 f 而变化:B(f) ~ I(f)。磁场(或者更加精确的说法是磁通密度及其相应磁场强度)随导体中心轴距离的增加而减弱。这些关系可以表示为:
以及
其中,B 为以第平方米伏秒 (V•s/m2) 表示的磁通密度,μ0 为自由空间中的磁导率(计算方法为 4π × 10–7 V•s/A•m),I 为以安培为单位的电流,r 为以米为单位的导体距离,而 H 为以安培每米 (A/m) 为单位的磁场强度。
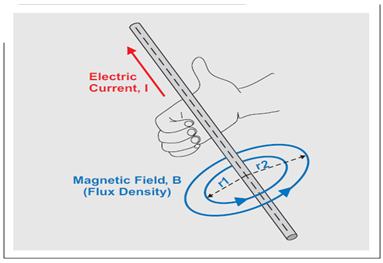
图 1 右手定则
磁场线穿过附近导体环路时,它们会产生一个 EMF,其强度大小取决于环路面积和通量密度及磁场频率:![]()
EMF 为以伏特为单位的电势,f 为磁场频率,而 A 为以平方米 (m2) 为单位的环路面积。
所有隔离器都有一定形状或者形式的导电环路,以让磁场线穿过并产生 EMF。如果强度足够大,则这种叠加到信号电压上的 EMF 就会导致错误数据传输。实际上,一些隔离技术对电磁干扰非常敏感。为了理解电容隔离器为什么不受磁场的影响,我们需要对其内部结构进行研究。
电容隔离器的结构
电容隔离器由两块硅芯片—一个发送器和一个接收机组成(请参见图 2)。数据传输在由两个电容构成的差动隔离层之间进行,在每个电容的二氧化硅 (SiO2) 电介质两端都有一块铜顶片和一个导电硅底片。发送器芯片的驱动器输出通过一些接合线连接到接收机芯片上隔离电容的顶片。通过将电容的底片连接接收机输入构成了一个导电环路。图 3 显示了隔离层的等效电路结构图,并标示出了金接合线之间的环路区域。很明显,穿过该环路的磁场将会产生一个 EMF,其表示下面 RC 网络的输入电压噪声 Vn1。我们常常碰到的第二种差动噪声部分 Vn2,其产生原因是共模噪声到差动噪声的转换。两个噪声分量共同组成了综合噪声 Vn。如果只考虑 EMF 的影响,则可以保守地将 Vn 一分为二:![]()

图 2 电容隔离器内部结构的简化结构图123下一页> 关键字:数字 电容 隔离器 磁场抗扰度 本文链接:http://www.cntronics.com/public/art/artinfo/id/80016504
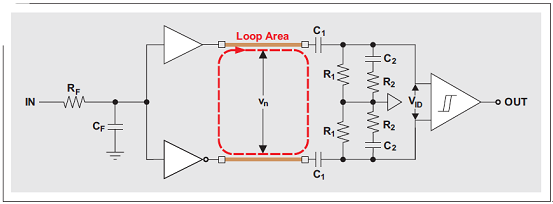
图 3 隔离层的等效电路结构图
若要触发接收机,RC 网络的输出必须提供一个差动输入电压 VID,其超出了接收机输入阈值。是否出现伪触发,具体取决于 RC 网络的增益响应 G(f)。
将差动网络转换为单端网络(请参见图 4),简化了 G (f) 的推导过程,但却要求 C′1 = 2C1,R′1= R1/2,C′2 = 2C2,以及 R′2 = R2/2。
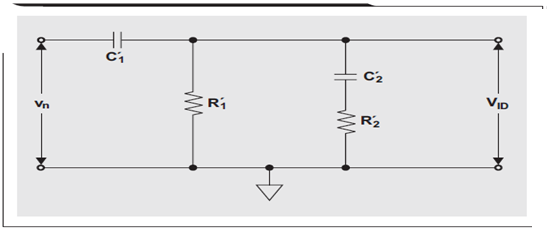
图 4 单端 RC 网络
一次电路仿真证实了 RC 网络为一个一阶高通滤波器,其 C′1 和 R′1 为主要组件,频率高达 100 MHz(参见图 5 中蓝色曲线)。超出这一频率以后,寄生组件 C′2 和R′2生效,从而引起稍稍偏离于线性的斜率。因此,频率达到 100 MHz 以后,增益响应可以表示为 VID/vn 的比:
确定不会引起伪接收机触发的最大允许噪声,要求对方程式 5 求解 vn: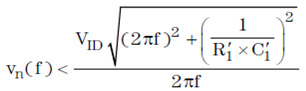
然后,将 vn 代入方程式 4,得到以伏特为单位的最大容许 EMF: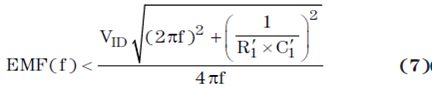
将 EMF 代入方程式 3,得到最大可能磁通密度:
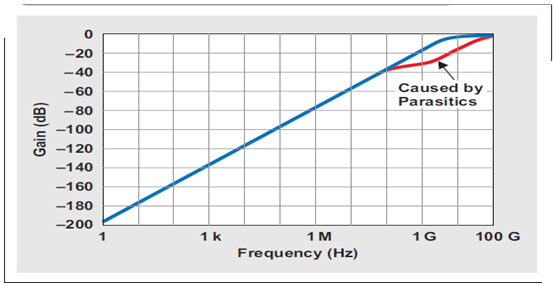
图 5 增益幅度频率响应 |G(f)|
<上一页123下一页> 关键字:数字 电容 隔离器 磁场抗扰度 本文链接:http://www.cntronics.com/public/art/artinfo/id/80016504?page=2
通过将下列数值插入方程式 8 中,推导出表 1 所列磁通密度的频变值:
VID = 10 mV(接收机输入阈值的大小)
R′1 × C′1 = 25 ps(有效时间常数)
A = 944 × 10–9 m2(有效环路面积)
f = 1 kHz to 100 MHz(相关频率范围)
表 1 距离电容隔离器 0.1m 的导体的电流值和磁场值
利用方程式 2 和 3 还得到 EMF、磁场强度 (H) 以及导体(此处假设将来的隔离器为 0.1 m)的相应电流 (I)。
由表 1 所列的一些极高值,清楚地表明 5 兆安低频电流和 100MHz 下 500A 电流都不能让这种隔离器停止正常工作。出现这种几乎无限 MFI 的原因是隔离电容的位置。如果这些电容位于发送器芯片上,则任何接合线中产生的 EMF 都能够影响到未受干扰的接收机输入。
很明显,这种高 MFI 值不可能进行实际的测试。电容隔离器的产品说明书说明了仅 1000 A/m 的适度值作为实际测试用。然而,无屏蔽电容隔离器可以轻松通过 IEC61000-4-8 和 IEC61000-4-9 标准的 5 级 MFI 要求。这些标准分别描述了高达 100 A/m 电源频率电磁场以及 1000 A/m 脉冲电磁场的应用。5 级规定了许多导体、总线或者中高压线路的恶劣工业环境,它们都携带有数万安的电流。另外还包括许多携带全部雷电电流的雷电保护系统和高层建筑结构(例如:电缆塔等)的接地导体。重型工业厂房和电站的室外配电装置也是这种环境的代表。
图 6 将电容隔离器的计算得 MFI 阈值同 IEC 61000-4-8 和 IEC 61000-4-9 的 5 级(最高)测试水平进行了对比。

图 6 MFI 测试阈值
结论
超出电容隔离器差动电路噪声预算的磁耦合要求 1MHz 下大于 11.7 V•s/m2(117千高斯) 的磁通量密度。这需要在一个距离器件 0.1m 的导体中有超过 5 百万安的电流才能产生这样一个磁场。在自然界或者任何制造设备中这都是不可能存在的。如果的确存在,那么设计人员便可做以下情况假设:在隔离层失效以前,周围的电路便都已失效。
