开关电源原理与设计(四)
中心议题:
- 反转式串联开关电源的工作原理
- 反转式串联开关电源储能电感的计算
- 反转式串联开关电源储能滤波电容的计算
反转式串联开关电源
反转式串联开关电源的工作原理
图1-7是另一种串联式开关电源,一般称为反转式串联开关电源。这种反转式串联开关电源与一般串联式开关电源的区别是,这种反转式串联开关电源输出的电压是负电压,正好与一般串联式开关电源输出的正电压极性相反;并且由于储能电感L只在开关K关断时才向负载输出电流,因此,在相同条件下,反转式串联开关电源输出的电流比串联式开关电源输出的电流小一倍。
在一般电路中大部分都是使用单极性电源,但在一些特殊场合,有时需要两组电源,其中一组为负电源。因此,选用图1-7所示的反转式串联开关电源作为负电源是很方便的。
图1-7中,Ui为输入电源,K为控制开关,L为储能电感,D为整流二极管,C为储能滤波电容,R为负载电阻。当控制开关K接通的时候,输入电源Ui开始对储能电感L加电,流过储能电感L的电流开始增加,同时电流在储能电感中也要产生磁场;当控制开关K由接通转为关断的时候,储能电感会产生反电动势,使电流继续流动,并通过整流二极管D进行整流,再经电容储能滤波,然后向负载R提供电流输出。控制开关K不断地反复接通和关断过程,在负载R上就可以得到一个负极性的电压输出。
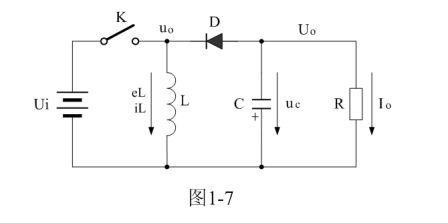
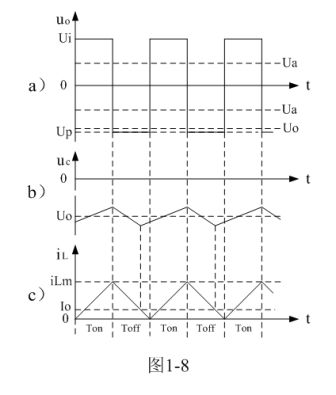
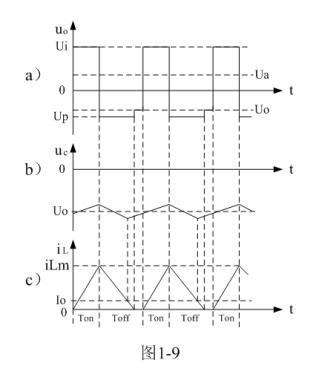
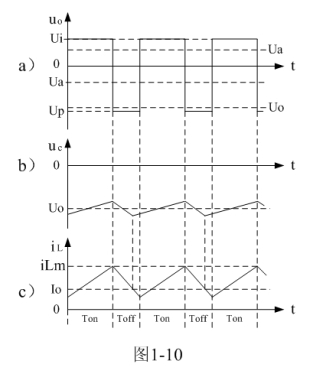
图1-8、图1-9、图1-10分别是控制开关K的占空比D等于0.5、< 0.5、> 0.5时,图1-7电路中几个关键点的电压和电流波形。图1-8-a)、图1-9-a)、图1-10-a)分别为控制开关K输出电压uo的波形;图1-8-b)、图1-9-b)、图1-10-b)分别为储能滤波电容两端电压uc的波形;图1-8-c)、图1-9-c)、图1-10-c)分别为流过储能电感L电流iL的波形。应该特别注意的是,图1-8-c)、图1-9-c)、图1-10-c)中的电流波形按原理应该取负值,但取负值后与前面图1-5与图1-6对比反而觉得不好对比和分析,因此,当进行具体计算时,一定要注意电流和电压的方向。
在开关接通Ton期间,控制开关K接通,电源Ui开始对储能电感L供电,在此期间储能电感L两端的电压eL为:

对(1-19)式进行积分得:
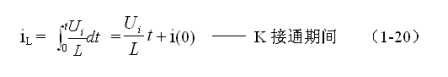
式中iL为流过储能电感L电流的瞬时值,t为时间变量;i(0)为的初始电流,即:控制开关K接通瞬间之前,流过储能电感L中的电流。当开关电源工作于临界连续电流状态时,i(0) = 0 ,由此可以求得流过储能电感L的最大电流为:

在开关关断Toff期间,控制开关K关断,储能电感L把电流iLm转化成反电动势,通过整流二极管D继续向负载R提供能量,在此期间储能电感L两端的电压eL为:
式中–Uo前的负号,表示K关断期间电感产生电动势的方向与K接通期间电感产生电动势的方向正好相反。对(1-22)式进行积分得:
式中i(Ton+)为控制开关K从Ton转换到Toff的瞬间之前流过电感的电流,i(Ton+)也可以写为i(Toff-),即:控制开关K关断或接通瞬间,之前和之后流过电感L的电流相等。实际上(1-23)式中的i(Ton+)就是(1-21)式中的iLm,即:
因此,(1-9)式可以改写为:

当t = Toff时iL达到最小值。其最小值为:

反转式串联开关电源输出电压一般为负脉冲的幅值。当开关电源工作于临界连续电流状态时,流过储能电感的初始电流i(0)等于0(参看图1-8-a)),即:(1-26)式中流过储能电感电流的最小值iLX等于0。因此,由(1-21)和(1-26)式,可求得反转式串联开关电源输出电压Uo为:
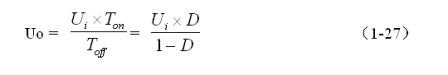
由(1-27)式可以看出,反转式串联开关电源输出电压与输入电压与开关接通的时间成正比,与开关关断的时间成反比。
另外,从图1-8可以看出,由于反转式串联开关电源,仅当控制开关K关断期间才产生反电动势向负载提供能量。因此,当占空比为0.5时,输出电流的平均值Io为流过储能电感电流最大值的四分之一;当占空比小于0.5时,输出电流的平均值Io小于流过储能电感电流最大值的四分之一(图1-9);当占空比大于0.5时,输出电流的平均值Io大于流过储能电感电流最大值的四分之一(图1-10)。
反转式串联开关电源储能电感的计算
反转式串联开关电源储能电感的计算方法与前面“串联式开关电源储能滤波电感的计算”方法基本相同,计算反转式串联开关电源中储能电感的数值,也是从流过储能电感的电流为临界连续电流状态进行分析。但须要特别注意,反转式串联开关电源中的储能电感仅在控制开关K关断期间才产生反电动势向负载提供能量,因此,流过负载的电流比串联式开关电源流过负载的电流小一倍,即:当占空比小于0.5时,反转式串联开关电源中流过负载R的电流Io只有流过储能电感L最大电流iLm的四分之一。根据(1-21)式:

(1-21)式可以改写为:

式中Io为流过负载的电流,当D = 0.5时,其大小等于最大电流iLm的四分之一;T为开关电源的工作周期,T正好等于2倍Ton。
由此求得:
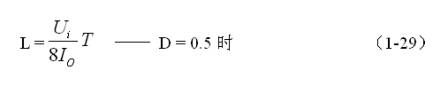
或:
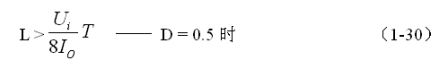
(1-29)和(1-30)式,就是计算反转式串联开关电源中储能电感的公式。同理,(1-29)和(1-30)式的计算结果,只给出了计算反转式串联开关电源储能滤波电感L的中间值,或平均值,对于极端情况可以在平均值的计算结果上再乘以一个大于1的系数。
当储能电感L的值小于(1-29)式的值时,流过滤波电感L的电流上升率将增大,如果流过滤波电感L的电流iL为连续电流,输出电压Uo将会升高;如果为了维持滤波输出电压Uo不变,则必须要把控制开关K占空比D减小,但占空比D的减小将会使流过储能电感的电流iL出现不连续,从而使滤波输出电压Uo的电压纹波增大。
如果流过滤波电感L的电流iL不是连续电流,储能电感L的减小,将会使流过储能电感的电流iL不连续的时间变长,电源滤波输出电压Uo不但不会升高,反而会使反转式串联开关电源滤波输出电压Uo的电压纹波显著增大。
当储能滤波电感L的值大于(1-29)式的值时,流过储能电感L的电流上升率将减小,输出电压Uo将降低,但滤波输出电压Uo的电压纹波显著减小;如果为了维持电源滤波输出电压Uo不变,控制开关K必须要把占空比D增大,而占空比D的增大又会使流过储能电感的电流iL不连续的时间缩短,或由电流不连续变成电流连续,从而使电源滤波输出电压Uo的电压纹波降低。
反转式串联开关电源储能滤波电容的计算
反转式串联开关电源储能滤波电容参数的计算,与串联式开关电源储能滤波电容的计算方法基本相同。但要注意,即使是在占空比D等于0.5的情况下,滤波电容器充、放电的时间都不相等,滤波电容器充电的时间小于半个工作周期,而电容器放电的时间则大于半个工作周期,但电容器充、放电的电荷是相等的,即电容器充电时的电流大于放电时的电流。这是整流滤波电路的普遍规律。
从图1-8可以看出,在占空比D等于0.5的情况下,电容器充电的时间为 ,电容充电电流的平均值为 ,或 ;而电容器放电的时间为 ,电容放电电流的平均值为0.9 Io。
因此有:
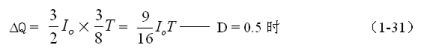
式中ΔQ为电容器充电的电荷,Io流过负载的平均电流,T为工作周期。电容充电时,电容两端的电压由最小值充到最大值(绝对值),相应的电压增量为2ΔUc,由此求得电容器两端的波纹电压ΔUP-P为:
由此求得:
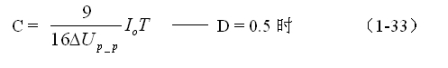
或:
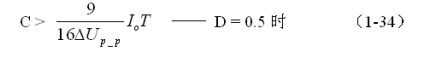
(1-33)和(1-34)式,就是计算反转式串联开关电源储能滤波电容的公式(D = 0.5时)。式中:Io是流过负载电流的平均值,T为开关工作周期,ΔUP-P为滤波输出电压的波纹,或电压纹波。一般波纹电压都是取电压增量的峰-峰值,因此,当D = 0.5时,波纹电压等于电容器充电的电压增量,即:ΔUP-P = 2ΔUc 。
同理,(1-33)和(1-34)式的计算结果,只给出了计算反转式串联开关电源储能滤波电容C的中间值,或平均值,对于极端情况可以在平均值的计算结果上再乘以一个大于1的系数。
当开关K的占空比D小于0.5时,由于流过储能滤波电感L的电流会不连续,电容器放电的时间将远远大于电容器充电的时间,因此,开关电源滤波输出电压的纹波将显著增大。另外,开关电源的负载一般也不是固定的,当负载电流增大的时候,开关电源滤波输出电压的纹波也将会增大。因此,设计开关电源的时候要留有充分的余量,实际应用中最好按(1-33)式计算结果的2倍以上来计算储能滤波电容的参数。
