开关变压器第十三讲:开关变压器漏感分析
开关变压器线圈之间存在漏感,是因为线圈之间存在漏磁通而产生的;因此,计算出线圈之间的漏磁通量就可以计算出漏感的数值。要计算变压器线圈之间存在的漏磁通,首先是要知道两个线圈之间的磁场分布。
任何变压器都存在漏感,但开关变压器的漏感对开关电源性能指标的影响特别重要。由于开关变压器漏感的存在,当控制开关断开的瞬间会产生反电动势,容易把开关器件过压击穿;漏感还可以与电路中的分布电容以及变压器线圈的分布电容组成振荡回路,使电路产生振荡并向外辐射电磁能量,造成电磁干扰。因此,分析漏感产生的原理和减少漏感的产生也是开关变压器设计的重要内容之一。
开关变压器线圈之间存在漏感,是因为线圈之间存在漏磁通而产生的;因此,计算出线圈之间的漏磁通量就可以计算出漏感的数值。要计算变压器线圈之间存在的漏磁通,首先是要知道两个线圈之间的磁场分布。
我们知道螺旋线圈中的磁场分布与两块极板中的电场分布有些相似之处,就是螺旋线圈中磁场强度分布是基本均匀的,并且磁场能量基本集中在螺旋线圈之中。另外,在计算螺旋线圈之内或之外的磁场强度分布时,比较复杂的情况可用麦克斯韦定理或毕-沙定理,而比较简单的情况可用安培环路定律或磁路的克希霍夫定律。
图2-30是分析计算开关变压器线圈之间漏感的原理图。下面我们就用图2-30来简单分析开关变压器线圈之间产生漏感的原理,并进行一些比较简单的计算。
在图2-30中,N1、N2分别为变压器的初、次级线圈,Tc是变压器铁芯。r是变压器铁芯的半径,r1、r2分别是变压器初、次级线圈的半径;d1为初级线圈到铁芯的距离,d2为初、次级线圈之间的距离。为了分析计算简单,这里假设变压器初、次级线圈的匝数以及线径相等,流过线圈的电流全部集中在线径的中心;因此,它们之间的距离全部是两线圈之间的中心距离,如虚线所示。
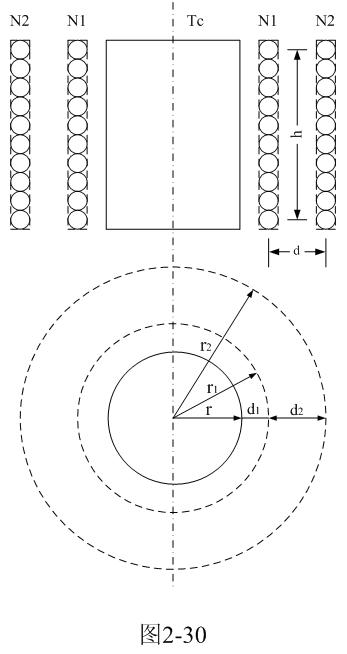


下面我们根据图2-30来简单计算变压器初、次级线圈之间的漏感Ls。

(2-97)式中,H为漏感的磁场强度;N为产生漏感线圈的匝数,这里N可以是N1或者N2;I为流过线圈N1或者N2的电流;h为两个线圈的高度。
如果我们拿(2-99)式与(2-67)式或(2-94)式进行对比,可以看出,线圈漏感与线圈的电感是没有本质区别的,只是磁路和磁通密度以及介质导磁率等参数需要根据实际情况来决定。
对于计算多层线圈的漏感可以用上述方法,逐层进行计算,然后求代数和;或者把多层线圈等效成一层,然后按单层来计算。实际中使用的变压器,其初、次级线圈的匝数不一定完全一样,导线的直径也不可能一样,还有线圈的高度也不可能一样,因此,精确计算每个线圈之间的漏感并不是一件很容易的事。
为了减少变压器初、次级线圈之间的漏感,在绕制变压器线圈的时候可以把初、次级线圈层与层之间互相错开,如图2-31所示。
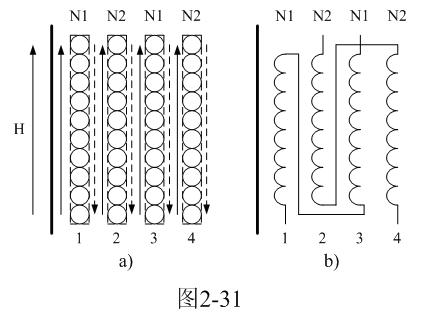
在图2-31中,两个线圈之间实线箭头表示正磁通的方向,虚线表示反磁通的方向。从图中可以看出,多层线圈间隙与间隙之间的正、反向磁通是可以部分抵消的,因此,变压器线圈的漏感可以减小。
例如:第2层线圈N2产生的正磁通,一部分落在第1层线圈N1的外面,属于漏磁通;但第2层线圈N2产生的反磁通,正好落在第3层线圈N1的里面;即:第2层次级线圈N2产生的正、反向磁通,正好落在初级线圈N1的第1层与第3层线圈之间,正、反向磁通的作用可以互相抵消。而第4层线圈N2产生的正、反向磁通,对第1层与第3层的初级线圈N1就没有太大的影响。
另外,从(2-99)式还可以看出,漏感的大小与两个线圈之间的距离还相关;如果把初、次级线圈用双平行或双交线来绕制,这样,两个线圈之间的距离就会变得小;特别是用双交线来绕制,相当于两层线圈不断交换里外位置,正、反向磁通互相抵消,因此,它们之间的漏感特别小。这种初、次级线圈采用双平行或双交线绕制的变压器一般多用于高频变压器,或脉冲变压器。但这种变压器初、次级线圈之间的绝缘强度不高,很难在大功率开关电源中使用。
一般变压器初、次级线圈的漏感大约在1~2%左右,如果采用分层错开绕制工艺,漏感可以降低到1%之下;若采用双交线绕制工艺,线圈漏感可以降低到5‰ 以下。
另外,线圈漏感相对值的大小还与变压器铁芯的气隙长度有关,这个用(2-99)式与(2-94)式进行对比就可以知道。变压器铁芯的气隙长度越大,其有效导磁率就越小,线圈漏感的相对值就越大。
对变压器线圈的漏感进行测试,方法很简单。例如,要测试变压器初级线圈的漏感,只需要把变压器所有次级线圈的两端进行短路,然后用仪表接到初级线圈的两端进行测试,其结果就是初级线圈的漏感。同理,需要对变压器次级线圈的漏感进行测试时,只需要把初级线圈的两端进行短路,然后用仪表接到次级线圈的两端进行测试,其结果就是次级线圈的漏感。
