圆柱形和矩形导体中的集肤效应:涡流和电流拥挤
【导读】根据您在涉及圆柱形底座的其他物理领域的经验,您可能已经正确猜测,当导线具有圆形横截面时,方程 1 的答案应包括贝塞尔函数。对于我们总是试图为不同现象开发简单模型的工程师来说,这不是一个好消息。贝塞尔函数可用于模拟各种物理问题,从圆柱形物体的热传导到描述鼓皮等圆形薄膜的振动。然而,它们可能很难可视化,并且显然比简单的指数衰减正弦波要简单得多。
圆柱形导体中的电流分布
我们可以求解良导体的麦克斯韦方程组,找到电流密度 J 的以下微分方程:
$$ abla ^2 J = j omega mu sigma J$$
等式 1。
如果您对向量微积分概念感到生疏,那么可怕的符号 ?2(Del 平方)被称为拉普拉斯算子。简而言之,拉普拉斯算子是多维空间中二阶导数概念的推广。它由下式给出:
$$ abla ^2 = frac{partial^2 }{partial x^2} + frac{partial^2 }{partial y^2} + frac{partial^2 }{partial z^2}$$
等式2。
方程 1 描述了良导体中的电流分布。它对于导电半空间和具有圆形横截面的导线均有效。然而,我们针对这两类媒体获得的解决方案是完全不同的。对于导电半空间,电流密度是一个简单的指数衰减正弦函数(如果我们假设我们正在处理平面波)。但是圆柱形导体呢?
根据您在涉及圆柱形底座的其他物理领域的经验,您可能已经正确猜测,当导线具有圆形横截面时,方程 1 的答案应包括贝塞尔函数。对于我们总是试图为不同现象开发简单模型的工程师来说,这不是一个好消息。贝塞尔函数可用于模拟各种物理问题,从圆柱形物体的热传导到描述鼓皮等圆形薄膜的振动。然而,它们可能很难可视化,并且显然比简单的指数衰减正弦波要简单得多。
由于这些函数的复杂性,我们不会详细分析分析的数学细节,而仅查看Simon Ramo 所著的《通信电子学中的场和波》一书中提供的结果。图 1 显示了四种不同频率下 1 毫米直径圆线横截面电流分布的归一化幅度。
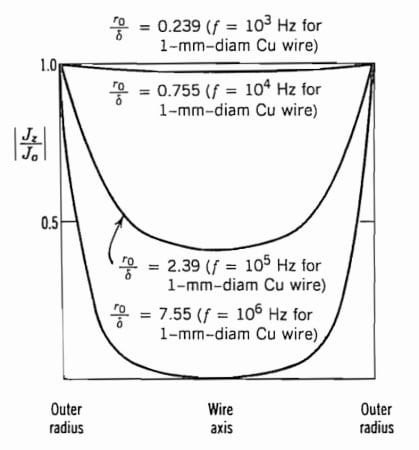
图 1.圆形导线中电流分布的归一化幅度。图片由S. Ramo提供
上图中的参数r0表示导线的半径。在频率 (f) 为 1 kHz 时,集肤深度约为导体半径的 4.2 倍(或等效 r0/δ = 0.239)。正如您所看到的,在这种情况下电流分布几乎是均匀的。
随着频率增加,趋肤深度减小,并且比率r0/δ从1kHz处的0.239增加至1MHz处的7.55。请注意,即使对于r0/δ=2.39,导线中心处的电流密度也几乎是导体表面处的电流密度的一半。这与集肤效应的简化描述不一致,集肤效应指出电流密度在δ深度处降低至其表面值的e-1 =0.37。
图 2 将 r 0/δ=2.39 和 r0/δ=7.55的实际电流分布与电流密度的指数衰减分布(对应于导电半空间中的波传播)进行了比较。正如您所看到的,只有当导体的曲率半径远大于趋肤深度时,半空间情况的结果才能用于近似圆线中的实际电流分布。
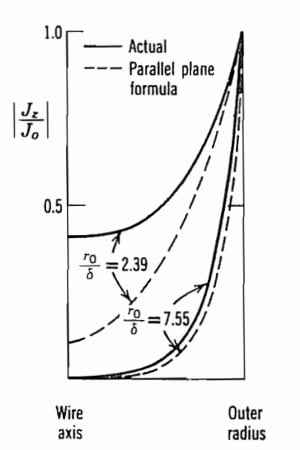
图 2.实际电流分布与平行平面公式的比较。图片由S. Ramo提供
根据经验,如果导体的所有曲率半径和厚度至少比趋肤深度大 3-4 倍,我们假设给定的导体类似于半无限块。到目前为止,在这个由两部分组成的系列中,我们依靠求解麦克斯韦方程组来描述集肤效应的一些重要的特征。通过观察法拉第感应定律如何在导体内部产生涡流,可以对这种效应有更深入(也许更有用)的了解。有了这种洞察力,我们就可以更好地理解不同互连的行为方式。
法拉第感应定律和涡流
根据法拉第定律,变化的磁场会在导线中感应出电动势(从而产生电流)。图 3(a) 中简单而熟悉的实验说明了该定律的基本思想。通过将磁铁靠近电线环,电线中会产生感应电动势,从而产生感应电流。
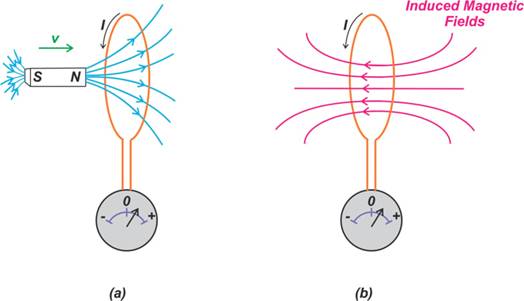
图 3.改变磁场会在导体中感应出电流
感应电动势与通过电路的磁通量的时间变化率成正比。此外,感应电流往往与初产生感应电流的原始磁通量的变化相反(楞次定律)。
图 3(b) 显示了当磁铁靠近线圈时产生的感应磁通量。感应磁场的方向是试图保持原始磁通量不发生变化。
什么是涡流?
正如变化的磁场可以在环路中感应出电流一样,当将大块金属置于变化的磁场中时,它也可以在大块金属中产生循环电流。这些循环电流称为涡流,如图 4 所示。
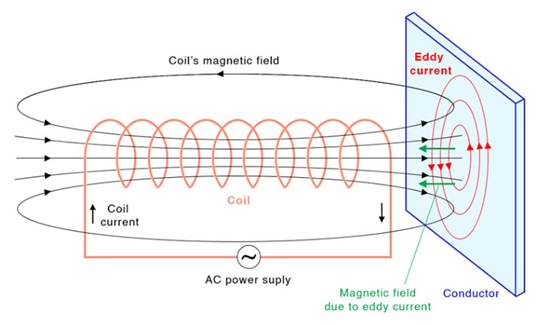
图 4.在导电平面中产生涡流。图片由Sciencefacts提供
再次注意感应电流的方向。假设线圈的磁场沿所描绘的方向增加,则感应出逆时针方向的电流以产生与线圈的原始磁场的变化相反的磁场。
载流导体内的涡流
当电流流过电线时,会在电线内部和外部产生磁场。对于交流电流,导线内部有一个随时间变化的磁场,根据法拉第定律,导线内部会产生涡流。如下图 5 所示。
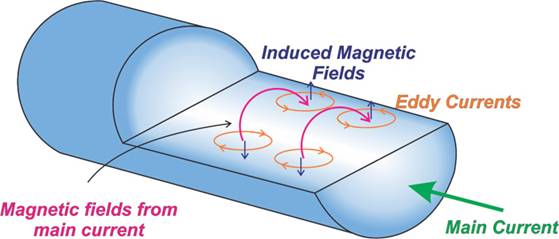
图 5.交流电流在电线中感应出涡流。
可以看出,涡流在导体表面附近沿主电流方向流动,但在导体内部沿相反方向流动。因此,靠近导体表面流动的总电流增加,而流过导体更深层的电流减少。
导体中的电流拥挤
应该注意的是,导体的某些表面可能比其他表面更有效地承载交流电流。为了理解这一点,请回想一下我们上面的讨论,变化的磁场会导致集肤效应。现在,如果导体的特定表面处的磁场更强,我们可以预期该表面将承载更大部分的电流。例如,考虑图 6 中所示的微带线的横截面。
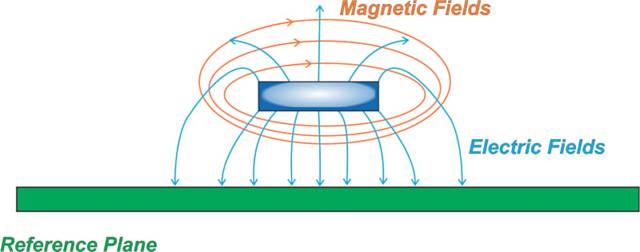
图 6.参考平面上微带线导体的横截面。
图 6 显示了微带线中电场和磁场的一般模式以及粗略的电流分布。请注意,这不是模拟结果。这只表明行为粗暴!
您是否注意到磁场更加集中在走线的底面和地平面之间?因此,微带线的底面比其顶面承载更多的电流。例如,大约 60% 的电流可能集中在线路横截面区域的深色阴影区域。由于相邻载流导体的影响而导致电流聚集在特定表面的现象称为邻近效应。
并行线路中的电流拥挤
当处理两根平行的圆柱形线时,观察到类似的效果(图 7)。在该图中,两个导体中的电流方向相反,因此导线之间的磁场强。结果,当前的人群聚集在彼此相对的表面上。

图 7.平行线的电流拥挤和邻近效应。图片由J. Davis提供
矩形导体中的电流拥挤
有趣的是,即使对于孤立的电线(没有邻近效应),导体的所有表面也可能不会承载相同量的电流。例如,细而宽的矩形导体的电流分布如图 8 所示。如您所见,垂直表面的电流密度大于水平表面。这是因为这些表面具有更强的磁场。
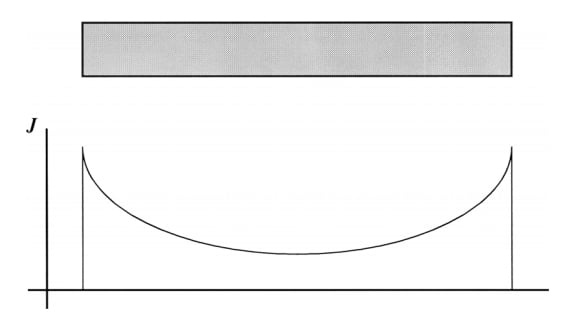
图 8.细矩形导线中的电流分布。图片由Thomas H. Lee提供
方形导体中的电流拥挤
从上面显示的薄矩形导体的结果中,您也许能够猜测方形导体的电流分布是什么样的。图 9 显示了方形横截面导体中的电流拥挤情况。四个角的电流密度。
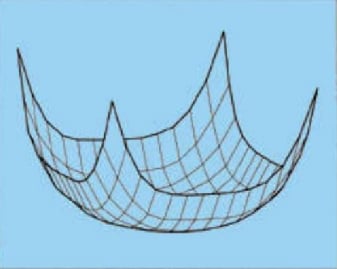
图 9.方形导体的电流分布。图片由艾伦·佩恩提供
不要忘记频率对当前拥挤的影响
正如我们在本文开头附近讨论的那样,电流分布和趋肤深度是频率的函数。当然,电流拥挤也取决于交流信号的频率。直流信号不会出现电流拥挤,并且会随着频率的增加而增加(直到某个点)。
由于电流拥挤,导体会遭受二次效应,需要在实际应用中考虑。导体的有效电阻可能比我们假设恒定电流分布时更高。电流拥挤还会导致导体中的热量和应力增加。当您创建使用时变信号的新设计时,始终考虑涡流和电流拥挤对电路性能的潜在影响。
免责声明:本文为转载文章,转载此文目的在于传递更多信息,版权归原作者所有。本文所用视频、图片、文字如涉及作品版权问题,请联系小编进行处理。
推荐阅读:
KWIK电路常见问题解答 15Msps 18位ADC的驱动器设计考虑因素
让频谱分析更高效,澄清RSA使用中的一些误解
功率因数校正基础知识
REASUNOS瑞森半导体高低压MOS在车载逆变器上的应用
如何设计低功耗、高精度自行车功率计
