抗混叠滤波器：将采样理论应用于 ADC 设计

【导读】到目前为止，我们已经探讨了奈奎斯特-香农定理的理论基础，包括频域对采样的影响。然后我们谈到了这些基本原则如何应用于现实生活中的电路设计——具体来说，解决了现实生活中混合信号系统中过采样的重要性。

到目前为止，我们已经探讨了奈奎斯特-香农定理的理论基础，包括频域对采样的影响。然后我们谈到了这些基本原则如何应用于现实生活中的电路设计——具体来说，解决了现实生活中混合信号系统中过采样的重要性。

在整个系列中，我使用的采样定理版本指出，当采样率等于或大于原始信号中频率的两倍时，完美重建是可能的——不是感兴趣的频率，也不是主频率，但频率。

这个看似无害的小细节实际上在理论采样和现实生活中的 A/D 转换之间造成了重大裂痕。

您的信号的频率是多少？

采样定理的个问题是您永远无法以频率的两倍进行采样：由于热噪声在太赫兹范围内具有恒定的功率谱密度，每个信号的带宽都远远超过模拟信号的能力- 到数字转换器。

当然，我并不是说所有信号在 1 THz 下都有一点噪声，因此混合信号电子设备不存在。相反，我试图戏剧性地证明不可能查看信号的傅里叶变换，绘制一条垂直线，并声明该线右侧的频谱完全为空。

噪声、干扰和自然现象的逐渐变化特征都会导致信号频谱没有容易识别的频率。

高频元件和混叠

为什么我们不能忽略那些麻烦的频率分量呢？我们不打算将它们数字化，我们不需要分析或记录它们——让我们忘记它们，根据我们想要的频率选择采样率吧！

我希望事情就这么简单，但我们必须记住，当模拟输入频率超过采样频率的一半时会导致混叠——顺便说一下，这有时被称为折叠频率，因为高于该频率的分量会围绕采样频率折叠从而与原始光谱重叠。我们不能简单地忽略折叠频率以上的成分，因为它们会与感兴趣的频率混合，从而消除我们完美重建原始信号的能力。

考虑下图：

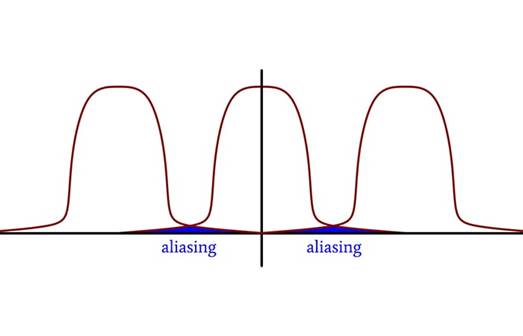
假设频谱的主要钟形部分包含感兴趣的频率，逐渐向零衰减的低幅度尾部代表不重要的高频分量。

该系统中选择的采样率足以捕获感兴趣的频率，但我们不能忽略不重要的频率，因为混叠会导致不重要的频率延伸到我们想要准确重建的频谱部分并使其失真。

然而，这种忽略不重要频率的想法实际上是我们如何在工程系统中处理这个问题的基础。归根结底，我们必须忽略不需要的高频，因为我们无法完全消除它们。但在我们忽略它们之前，我们至少应该做出一些努力来减轻它们对系统性能的有害影响。

这就是抗混叠滤波器发挥作用的地方。

采样前过滤

香农采样定理指定了相对于信号频率的可接受采样率。另一种说法是，香农给了我们带限信号的采样率要求，即傅立叶变换具有可识别上限的信号。

我们在物理电路中发现的信号并不是真正的带限信号，但我们无论如何都要对它们进行采样，因此，我们将尝试使它们成为带限信号。这就是抗混叠滤波器的目的。

通过在采样前让信号通过低通滤波器，我们可以衰减指定频率以上的频谱内容，从而创建频率上限。

信号不会完全受限，因为现实生活中的滤波器不会在截止频率以上产生无限衰减。然而，它可以足够接近带宽限制：混叠会发生，但它对整体系统性能的影响可以忽略不计。

我们如何选择截止频率？

这将取决于各种因素。一般的想法是保留频谱的重要部分并抑制不重要的部分。然后，您可以根据希望将混叠到感兴趣的频谱中的频率分量衰减多少来选择 ADC 采样率。

假设您正在为抗混叠滤波器使用一阶RC 低通滤波器，截止频率为 20 kHz。频率响应如下所示：

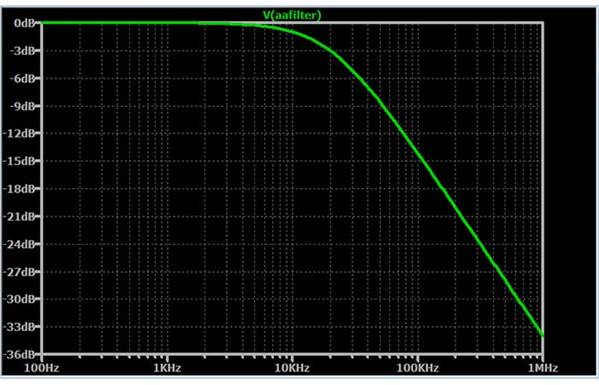
如果您以 100 kHz 采样，则折叠频率为 50 kHz：高于 50 kHz 的所有频率都会导致混叠误差。因此，使用这个滤波器，“混叠带”将有 9 dB 的衰减。

够了吗？

这个问题没有简单的答案，无论如何，答案取决于系统要求。

尽管如此，我的工程直觉告诉我，我们应该努力将混叠带的幅度降低至少一个数量级。这个一阶 RC 滤波器在 200 kHz 时为我们提供 20 dB 的衰减，因此我们需要以 400 kHz 进行采样。在我喜欢使用的 ADC 的背景下，这是一个相当高的采样率——即那些可以方便地集成到微控制器中的 ADC 。因此，我可能不得不放宽衰减要求，或者我可以考虑为抗混叠滤波器使用二阶拓扑。

结论

顾名思义，抗混叠滤波器可减少我们对信号进行采样时发生的混叠量。他们通过抑制折叠频率以上的频谱内容来做到这一点，从而使现实生活中的信号与香农采样定理适用的带限信号更加一致。

虽然您可以通过提高采样率来降低抗混叠滤波器的重要性，但我认为在您的 ADC 电路中始终至少包含一个基本 RC 滤波器是一种很好的做法。

免责声明：本文为转载文章，转载此文目的在于传递更多信息，版权归原作者所有。本文所用视频、图片、文字如涉及作品版权问题，请联系小编进行处理。