大脑如何感知时间的流逝?
生命系统从根本上是不可逆的,它们打破细致平衡,建立了时间之箭。但是,整个系统的时间之箭是如何从多个元素的相互作用中产生的?在近日发表于?PRL?和?PRE?的两篇论文中,研究人员证明了复杂相互作用系统中时间之箭的局部证据,即热力学系统的熵增是可以分解的。
他们在噪声逻辑计算的简单模型上说明了这种分解,然后将其应用到视网膜神经活动模式的分析中,证明神经活动的不可逆性来自于神经元对之间的相互作用。
本文来自微信公众号:集智俱乐部 (ID:swarma_org),作者:Yasser?Roudi等,译者:潘佳栋,原文标题:《PRL前沿:分解大脑中的局部时间之箭》,头图来自:电影《星际穿越》剧照
一、复杂生物系统中的时间之箭
破碎的鸡蛋不能自发复原,一滴墨水一旦混入水中就不能自发分离。自然界充满了这种不可逆的现象,这些行为本身无法逆转。这种不可逆性由熵产生率(entropy production rate)来量化,根据热力学第二定律,熵增始终非负[1]。
因此,人们可以把熵产生率看作是一个系统时间流动或“箭头”的度量。然而,对于复杂系统(比如大脑)来说,测量这个参数是很困难的,因为它们的组成元素之间存在着非平凡且复杂的相互作用。
最近,纽约城市大学和普林斯顿大学的 Christopher Lynn 及其同事提出了一种量化这种系统中熵产生率的方法 [2,3](图1)。该团队将其方法应用于蝾螈视网膜中神经元的活动,当系统对一系列复杂的视觉图像做出反应时。他们的工作为定量分析复杂生物系统中的时间之箭打开了大门,例如大脑中的神经元网络,在那里,该模型能够让我们对时间流逝的感知神经基础有一个定量理解。

图1:研究人员已经开发出一种方法来计算复杂系统行为的不可逆性。
二、计算不可逆性
在基本层面上,系统的不可逆性在数学上等价于系统在两个状态之间转换的概率与反向转换的概率之间的“距离”[4]。当这些概率不同时,距离为正。如此定义的不可逆性不是一个全有或全无的量;它可以有任何正值。从真实系统的数据中估计该值可能非常困难,特别是对于生物系统,其中大多数系统非常复杂,并且有许多相互作用的变量。
例如,大脑中有数十亿个神经元——大脑的信息信使,它们发出微小的电压,以产生不同的电压棘波模式——大脑的状态。即使在一毫米尺寸的大脑中,也有数千个神经元,这使得测量变得很棘手。
目前的实验技术只允许科学家以高时间分辨率记录几百个左右神经元的棘波序列。然而,棘波序列不能被记录足够长的时间,以允许计算互连神经元网络的不可逆性。因此,需要一种适用于我们现有的有限数据的方法来计算不可逆性。这就是 Lynn 和他的同事们要解决的问题。
在他们的研究中,Lynn 及其同事证明,在诸如大脑这样的系统中,不可逆性可以分解为一系列项,这些项可以从一阶统计、二阶统计、三阶统计,直到N阶统计中计算,其中N是变量的个数。在大脑的情况下,这些项对应于单个神经元、神经元对、三个神经元等的棘波统计数据的贡献。
该团队证明,这种分解可以用于计算一些简单小型模型的不可逆性,并对整个系统进行评估。例如,该团队将其模型应用于布尔逻辑门系统,该系统对多个二进制输入执行操作,生成单个二进制输出。他们还考虑了一个神经元理论系统,可以产生今天可记录的长度的棘波序列。
在这种情况下,他们发现能够准确估计低阶统计量,但不能准确估计高阶统计量——随着阶数的增加,计算需要越来越多的数据,准确估计变得不可能。这一发现表明,如果对于给定的系统级数收敛得足够快,则可以使用该形式合理地计算不可逆性。
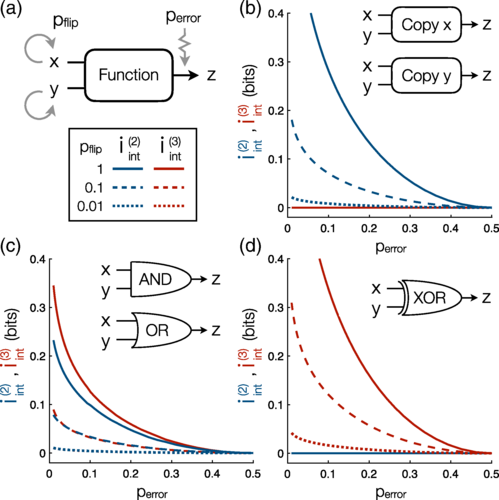
图2:分解逻辑函数的不可逆性:
(a) 由三个二进制变量x、y和z组成的系统,其中z在输入x和y上执行一个有噪声的逻辑函数。在每个时间点,其中一个变量随机更新。
(b)-(d) 对不同逻辑函数的局部时间箭头的二阶和三阶贡献。在所有函数中,不可逆性随错误率升高而降低。
(b) 当z复制x或y时,三元组不可逆性消失,所有不可逆性都来自二阶动力学。
(c) 对于与和或,不可逆性由二阶动力和三阶动力学驱动。
(d) 对于异或,二阶的不可逆性消失,所有的不可逆性都产生于三阶动力学。
三、测量神经活动的不可逆性
在神经数据方面,Lynn 和同事们还将他们的方法应用于从蝾螈视网膜在受到不同视觉刺激时的棘波序列记录:一个自然风景的电影,和显示布朗运动的人工构建的可逆电影。他们表明,他们的数据足以估计五阶或六阶统计量,这意味着只有当一个系统包含多达五个或六个神经元时,才能进行完整的分析。
然后,研究小组对该系统进行了以下观察:首先,测得的不可逆程度取决于所播放的电影。其次,即使刺激是可逆的,不可逆性也总是正的,这一发现表明棘波序列的不可逆性不仅仅来源于刺激。
这两个结果都不特别令人惊讶,考虑到视网膜是一个生物机器,它对视觉刺激的统计数据做出反应,但并不完全复制这些统计数据,因此可以预期后一结果。也许令人惊讶的是,当刺激可逆时,棘波序列的不可逆性比不可逆时更大。
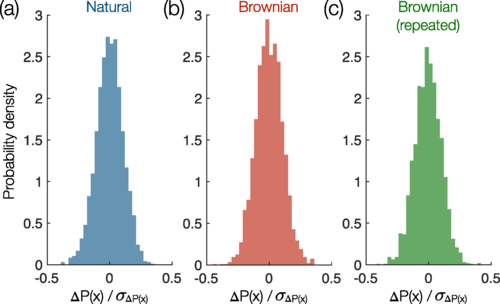
图3:神经元在随机稳定状态下工作。(a-c) 表示状态概率变化的分布。
该团队还发现,低阶(尤其是二阶)统计数据占估计总不可逆性的大部分。如果这个结果适用于更大的神经元群体,那将是一个好消息,因为实验人员可以简单地使用低阶统计数据来获得他们所需的信息,而不必使用越来越高的阶。
然而,这种可能性并不明显,因为N阶相关性的数量随着种群规模呈指数增长,所以它们对较大群体的影响可能更显著[5]。最终,甚至有可能将该模型应用到足够大的具有行为相关性的网络上,从而使研究人员能够解决诸如主观感知的时间流逝,是否或如何与网络动力学中的不可逆性相关等问题。
当然,测试这些问题的实验还不可能。然而,随着目前在数据收集和复杂系统操作方面取得的显著技术进步,这种情况可能很快就会改变。Lynn 及其同事的定量框架将有助于设计和分析此类实验。
参考文献
[1]E. Fermi,?Thermodynamics?(Dover Publications, New York, 1936).
[2]C. W. Lynn?et al., “Decomposing the local arrow of time in interacting systems,”?Phys. Rev. Lett.?129, 118101 (2022).
[3]C. W. Lynn?et al., “Emergence of local irreversibility in complex interacting systems,”?Phys. Rev. E?106, 034102 (2022).
[4]U. Seifert, “Stochastic thermodynamics, fluctuation theorems and molecular machines,”?Rep. Prog. Phys.?75, 126001 (2012).
[5]Y. Roudi?et al., “Pairwise maximum entropy models for studying large biological systems: When they can work and when they can’t,”?PLoS Comput. Biol.?5, e1000380 (2009).
本文来自微信公众号:集智俱乐部 (ID:swarma_org),作者:Yasser?Roudi等,译者:潘佳栋,本文翻译自 physics.aps.org,原文题目:Decomposing the Local Arrow of Time in the Brain,原文链接:https://physics.aps.org/articles/v15/133
