Discovery Helps Computers Draw Intricate Two-Dimensional Animations

Nearly 60 years ago computer scientist Ruth Weiss of Bell Labs published a pioneering algorithm to turn three-dimensional objects into two-dimensional drawings from any angle. But she ran into a problem with depicting outlines—an issue that has remained a computational geometry riddle for decades. With the ubiquity of computer animation today, this “hidden line problem” is now even more pressing.

The trickiest part of rendering a 3-D model in 2-D, a crucial step in computer animation, is the deceptively simple matter of the contour: the 2-D visual outline of the 3-D object. In a perfect world, a contour could be delineated with infinite precision—but the real world demands finite values. So modern algorithms start by covering the entire 3-D model with a mesh of tiny triangular “tiles,” then determining whether each tile would be facing a viewer or facing away. Next, algorithms use these tiles to build line segments that serve as the contour. But the results can create faulty, flickering lines when used in a stylized animation—and researchers were unsure why.

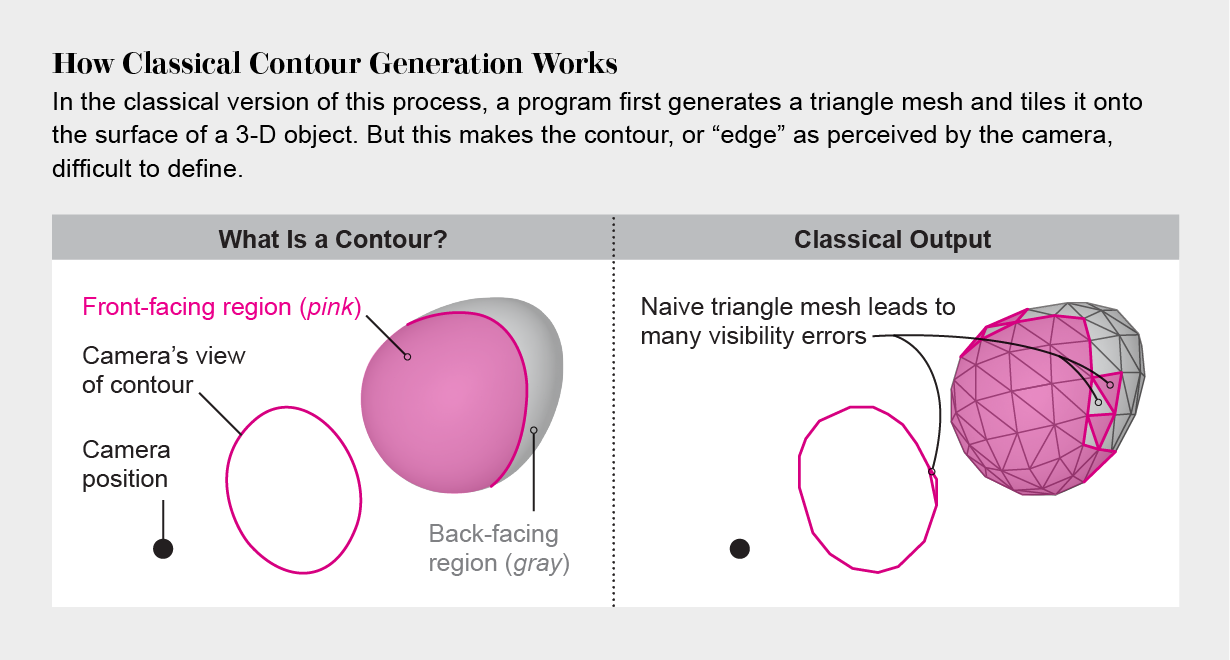
It has proved impossible to generate a triangle mesh fine enough to avoid every error of this kind. As Meta Reality Labs researcher Stéphane Grabli, an Oscar nominee for visual effects, explains, “The feeling was that with enough subdivision, it should be possible to create a mesh that allows exact visibility computation for these contours. This turned out to be wrong.” The resulting errors limit the complexity of nonphotorealistic illustration styles, Grabli adds.

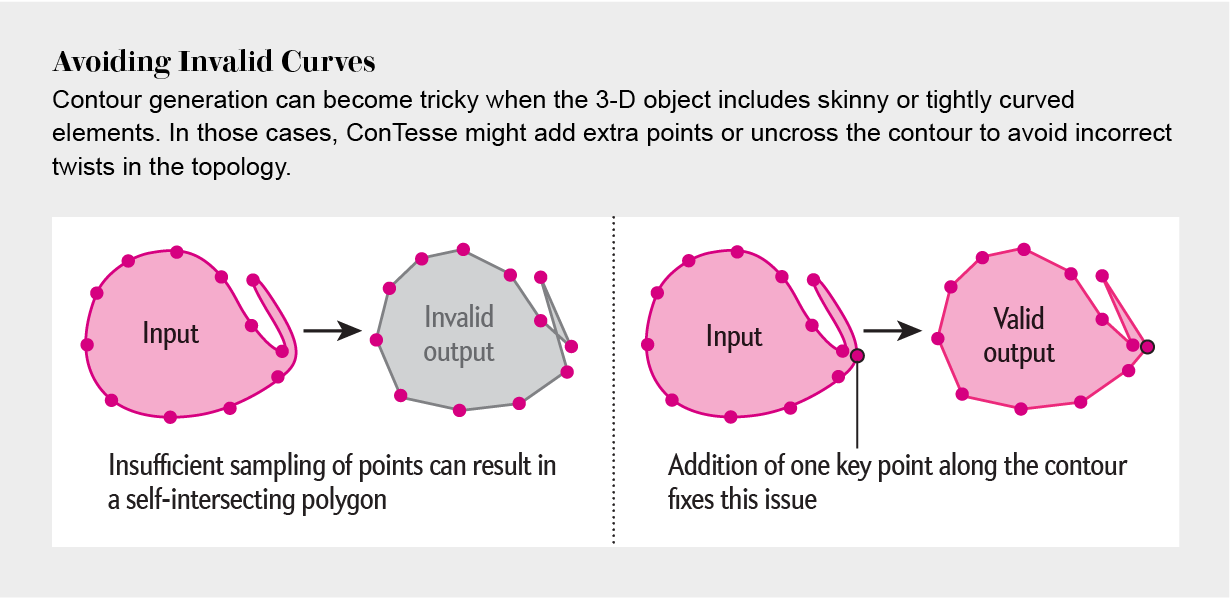
Now, in ACM Transactions on Graphics, University of British Columbia computer scientist Chenxi Liu and her colleagues propose an algorithmic solution, called ConTesse, that focuses on fixing the contour rather than the mesh. Zooming in by a factor of 1,600 on algorithm-generated contours, Liu identified small twists where the contour lines incorrectly crossed one another—and thus the tiles could not be consistently identified as facing toward or away from the viewer. “I experimented with many surfaces and saw that the algorithm failed on most of them,” she says.

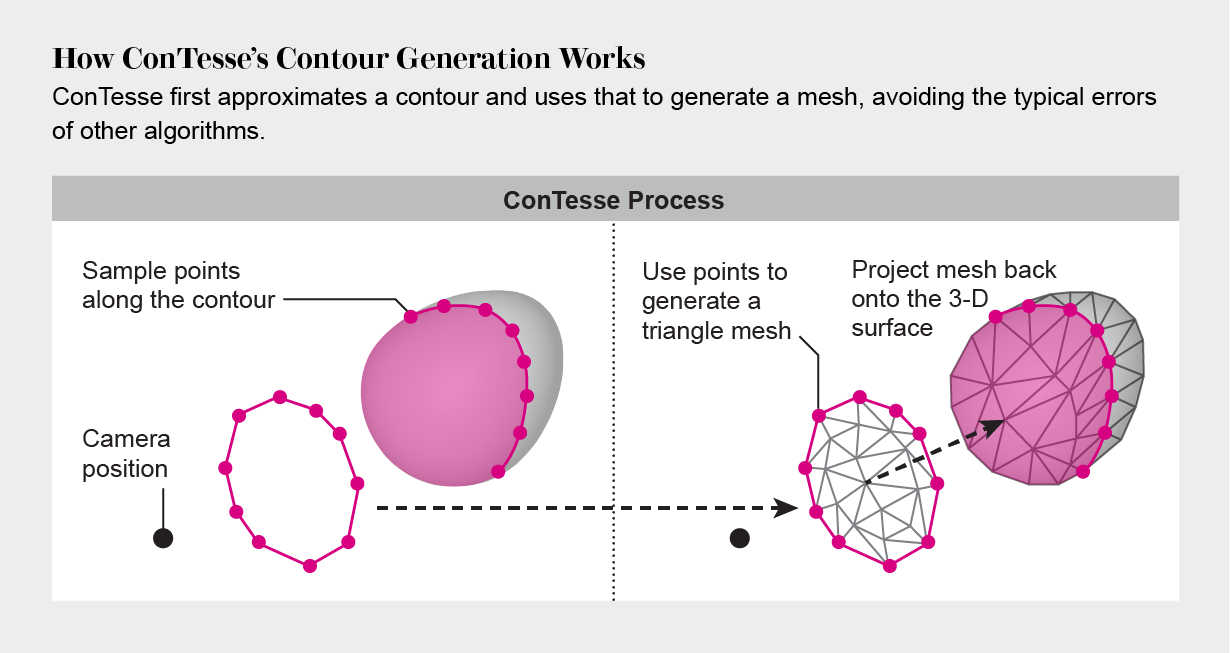
The researchers’ new algorithm first traces a 3-D shape’s edges with line segments, then squashes this approximate contour down to 2-D and tries to tile its interior with triangles. Wherever that interior mesh mistakenly crosses over itself, the algorithm modifies that part of the contour, such as by untwisting it or adding finer line segments. The algorithm then regenerates the mesh using the repaired contour and projects it all back onto the 3-D object for a final visibility check.

The team’s innovation was to realize that the problem was with the contour itself. Previously it was unclear that such invalid contours were even possible, so fixes treated the flickering symptoms rather than the cause, Liu says. Grabli, who was not involved in the new research, concurs: “The paper proves why early solutions couldn’t work.”