绝对式光电编码器

绝对式光电编码器基本构造及特点

用增量式光电编码器有可能由于外界的干扰产生计数错误，并且在停电或故障停车后无

法找到事故前执行部件的正确位置。采用绝对式光电编码器可以避免上述缺点。绝对式光电

编码器的基本原理及组成部件与增量式光电编码器基本相同，也是由光源、码盘、检测光栅、

光电检测器件和转换电路组成。与增量式光电编码器不同的是，绝对式光电编码器用不同的

数码来分别指示每个不同的增量位置，它是一种直接输出数字量的传感器。在它的圆形码盘

上沿径向有若干同心码道，每条上由透光和不透光的扇形区相间组成，相邻码道的扇区数目

是双倍关系，码盘上的码道数就是它的二进制数码的位数，在码盘的一侧是光源，另一侧对

应每一码道有一光敏元件；当码盘处于不同位置时，各光敏元件根据受光照与否转换出相应

的电平信号，形成二进制数。这种编码器的特点是不要计数器，在转轴的任意位置都可读出

一个固定的与位置相对应的数字码。显然，码道越多，分辨率就越高，对于一个具有 N 位

二进制分辨率的编码器，其码盘必须有N 条码道。绝对式光电编码器原理如图1-8 所示。

绝对式光电编码器是利用自然二进制、循环二进制（格雷码）、二-十进制等方式进行光

电转换的。绝对式光电编码器与增量式光电编码器不同之处在于圆盘上透光、不透光的线条

图形，绝对光电编码器可有若干编码，根据读出码盘上的编码，检测绝对位置。它的特点是：

可以直接读出角度坐标的绝对值；没有累积误差；电源切除后位置信息不会丢失；编码器的

精度取决于位数；最高运转速度比增量式光电编码器高。

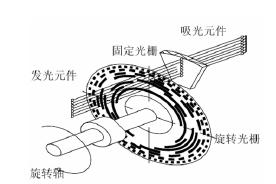
图1-8 绝对式光电编码器原理

1.3.2 码制与码盘

绝对式光电编码器的码盘按照其所用的码制可以分为：二进制码、循环码（格雷码）、

十进制码、六十进制码（度、分、秒进制）码盘等。四位二元码盘（二进制、格雷码）如图

1-9 所示。图中黑、白色分别表示透光、不透光区域。

图 1-9 四位二元码盘

图 1-9（a）是一个四位二进制码盘，它的最里圈码道为第一码道，半圈透光半圈不透光，

对应于最高位C1，最外圈为第n 码道，共分成2n 个亮暗间隔，对应于最低位Cn，n 位二元

码盘最小分辨率为：

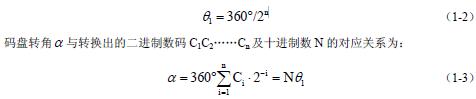
二进制马盘的缺点是：每个码道的黑白分界线总有一半与相邻内圈码道的黑白分界线是

对齐的，这样就会因黑白分界线刻画不精确造成粗误差。采用其他的有权编码时也存在类似

的问题。图1-10 是一个四位二进制码盘展开图，图中aa 为最高位码道黑白分界线的理想位

置，它与其他三位码道的黑白分界线正好对齐，当码盘转动，光束扫过这一区域时，输出数

码从0111 变为1000 不会出现错误。如果C1 道黑白分界线刻偏到a’a’，当码盘转动时，输

出数码就会从0111 变为1111 再变到1000，中途出现了错误数码1111。反之C1 道黑白分界

线刻偏到a’’a’’，当码盘转动时，输出数码就会从0111 变为0000 再变到1000，中途出现了

错误数码0000。为了消除这种粗误差，可以采用循环码盘（格雷码盘）。

图 1-9（b）是一个四位循环码盘，它与二进制码盘相同的是，码道数也等于数码位数，

因此最小分辨率也是式（1-2）求得，最内圈也是半圈透光半圈不透光，对应R1 位，最外圈

是第n 码道对于Rn 位。与二进制码盘不同的是：第二码道也是一半透光一半不透光，第i

码道分为2i-1个黑白间隔，第i 码道的黑白分界线与第i-1 码道的黑白分界线错开360° / 2i。

循环码盘转到相邻区域时，编码中只有一位发生变化。只要适当限制各码道的制作误差和安

装误差，就不会产生粗误差。由于这一原理，使得循环码盘获得广泛的应用。

1.3.3 二进制码与循环码的转换

绝对式光电编码器是利用自然二进制或循环二进制（格雷码）方式进行光电转换的，编

码的设计一般是采用自然二进制码、循环二进制码、二进制补码等。特点是不要计数器，在

转轴的任意位置都可读出一个固定的与位置相对应的数字码；抗干扰能力强，没用累积误差；

电源切断后位置信息不会丢失，但分辨率是由二进制的位数决定的，根据不同的精度要求，

可以选择不同的分辨率即位数。目前有10 位、11 位、12 位、13 位、14 位或更高位等多种。

其中采用循环二进制编码的绝对式编码器，其输出信号是一种数字排序，不是权重码，

每一位没有确定的大小，不能直接进行比较大小和算术运算，也不能直接转换成其他信号，

要经过一次码变换，变成自然二进制码，再由上位机读取以实现相应的控制。而在码制变换

中有不同的处理方式，本文着重介绍二进制格雷码与自然二进制码的互换。

（1）格雷码（又叫循环二进制码或反射二进制码）介绍

在数字系统中只能识别 0 和1，各种数据要转换为二进制代码才能进行处理，格雷码是

一种无权码，采用绝对编码方式，典型格雷码是一种具有反射特性和循环特性的单步自补码，

它的循环、单步特性消除了随机取数时出现重大误差的可能，它的反射、自补特性使得求反

非常方便。格雷码属于可靠性编码，是一种错误最小化的编码方式，因为，自然二进制码可

以直接由数/模转换器转换成模拟信号，但某些情况，例如从十进制的3 转换成4 时二进制

码的每一位都要变，使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点，它是

一种数字排序系统，其中的所有相邻整数在它们的数字表示中只有一个数字不同。它在任意

两个相邻的数之间转换时，只有一个数位发生变化。它大大地减少了由一个状态到下一个状

态时逻辑的混淆。另外由于最大数与最小数之间也仅一个数不同，故通常又叫葛莱反射码或

循环码。表1-1 为几种自然二进制码与格雷码的对照表：

表 1-1 几种自然二进制码与格雷码的对照表

从表 1-1 种可以得出，十进制数N 与n 位二进制码满足以下关系：

可见，二进制码由于是有权码，满足（1-4）的关系，而格雷码是无权码，不满足（1-4）

的关系。它与所对应的角度不存在类似（1-3）的关系，因此必须找出循环码和二进制码之

间的对应关系和相互转换规则。

（2）二进制码转换成制格雷码

二进制码转换成制格雷码，其法则是保留二进制码的最高位作为格雷码的最高位，而次

高位格雷码为二进制码的高位与次高位相异或，而格雷码其余各位与次高位的求法相类似。

图1-11 所示为二进制码转换成格雷码。

图 1-11 自然二进制码转换成二进制格雷码

图 1-12 为将二进制码转换为格雷码的电路图，其中图（a）为并行转换电路，图（b）

为串行转换电路。当采用串行电路时，工作之前先将D 触发器D1 置0，Q=0，在Ci 端送入

C1，异或门D2 输出R1=C1○+ 0=C1，随后加CP 脉冲，使Q=C1；在Ci 端加入C2，D 输出R2=C2○+

C1，以后重复上述过程，可以依次获得R1，R2，……，Rn。

（3）格雷码转换为二进制码

格雷码转换成二进制码，则是保留格雷码的最高位作为二进制码的最高位，而次高位二

进制码为高位二进制码与次高位格雷码相异或，而二进制码的其余各位与次高位二进制码的

求法相类似。图1-13 为将格雷码转换为二进制码的电路，其中图（a）为并行转换电路，图

（b）为串行转换电路。当采用串行电路时，工作之前先将JK 触发器D 置0，Q=0，将R1

同时加到J、K 端，再加入CP 脉冲后，Q=C1= R1。以后若Q 端为Ci-1 在J、K 端加入Ri。

根据JK触发器的特性，若J、K为“1”则加入CP脉冲后， i 1 Q C − = ；若J、K 为“0”则

加入CP 脉冲后保持Q=Ci-1。这一逻辑关系可以写成：

图 1-13 格雷码转换为二进制码的电路

格雷码是无权码，采用格雷码盘获得的格雷码R1，R2，……，Rn 必须按图1-11 转换为

对应的二进制码C1，C2，……，Cn 后，才能代入（1-3）式确定与之对应的角度。

（4）格雷码与二进制码互换的软件实现方法

（a）二进制码转换成格雷码的软件实现法

根据自然二进制转换成格雷码的法则，可以得到以下的代码：

staTIc unsigned int DecimaltoGray(unsigned int x)

{

return x^(x>>1);

}

//以上代码实现了unsigned int 型数据到格雷码的转换，最高可转换32 位自然二进

制码，超出32 位将溢出。

staTIc int DecimaltoGray( int x)

{

return x^(x>>1);

}

//以上代码实现了 int 型数据到格雷码的转换，最高可转换31 位自然二进制码，超

出 31 位将溢出。

上述代码即可用于 VC 控制程序中，也可以用于单片机控制程序中。在单片机程序设计

时，若采用汇编语言编程，可以按相同的原理设计程序；若采用C 语言编程，则可以直接

利用上述代码，但建议用unsigned int 函数。

（b）软件实现法(参见示例工程中的 Gray to Binary )

根据二进制格雷码转换成自然二进制码的法则，可以得到以下的三种代码方式：

staTIc unsigned int GraytoDecimal(unsigned int x)

{

unsigned int y = x;

while(x>>=1)

y ^= x;

return y;

}

staTIc unsigned int GraytoDecimal(unsigned int x){

x^=x>>16;

x^=x>>8;

x^=x>>4;

x^=X>>2;

x^=x^1;

return x;

}

static unsigned int GraytoDecimal(unsigned int x)

{

int i;

for(i=0;(1<<i)<sizeof(x)*8;i++)

{

x^=x>>(1<<i);

}

return x;

}

//以上代码实现了unsigned int 型数据到自然二进制码的转换，最高可转换32 位格雷码，

超出32 位将溢出。将数据类型改为int 型即可实现31 位格雷码转换。

上述代码即可用于 VC 控制程序中，也可以用于单片机控制程序中。在单片机程序设计

时，若采用汇编语言编程，可以按相同的原理设计程序；若采用C 语言编程，则可以直接

利用上述代码，但建议用unsigned int 函数。

更详细请查看: https://bbs.elecfans.com/dispbbs_54_113406.html