自组织映射神经网络（SOM）实战 译文

译者 |?朱先忠

审校 |?孙淑娟

自组织映射的演变迭代gif动画示意图

1. 简介

自组织映射（SOM）是由芬兰赫尔辛基理工大学的Teuvo Kohonen在20世纪80年代提出的一种无监督机器学习算法（参考文献1）。顾名思义，映射是在没有他人指示的情况下自行组织的。这是一个受大脑神经网络活动启发而发明的模型。大脑皮层的另一个区域负责特定的活动。视觉、听觉、嗅觉和味觉等感觉输入通过突触以自组织方式映射到相应皮层区域的神经元。众所周知，输出相似的神经元是邻近的。SOM通过竞争性神经网络进行训练，这是一种类似于这些大脑机制的单层前馈神经网络。

SOM算法相对简单，但乍一看可能会有一些混乱，并且难以确定如何在实践中应用它。这可能是因为SOM可以从多个角度理解的缘故吧。它类似于用于降维和可视化的主成分分析（PCA：一种通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量的统计方法）。自组织映射也可以被视为一种处理非线性降维的流形学习。SOM还因其矢量量化特性而应用于数据挖掘领域（参考文献2）。该序列可以将高维可观察数据表示到低维潜在空间，通常在二维正方形网格上，同时保留原始输入空间的拓扑结构。但映射也可以用于投影新的数据点，并查看哪个簇属于映射。

本文将努力解释自组织映射的基本架构及其算法，并重点介绍其自组织方面。我们将使用基于Python的UCI机器学习库（参考文献3）中可用的数据集来开发一个SOM模型以解决聚类问题。然后，我们将看到映射在在线（连续）培训期间是如何自组织的。最后，我们还会评估经过训练的自组织映射，并讨论其优点和局限性。尽管SOM不是当下最流行的ML技术，在学术文献之外也不太常见；然而，并没有结论说，SOM不是解决所有问题的有效工具。训练模型相对容易，训练模型的可视化有助于向非技术类人员，例如审计师们，作出更直观有效的解释。我们将看到，该算法面临的问题通常也完全可以在其他无监督方法领域中共享。

2. 架构和学习算法设计

自组织映射的神经网络有一个输入层和一个输出层。第二层通常由m x n个神经元的二维网格组成。映射层的每个神经元与输入层的所有神经元紧密连接，具有不同的权重值。

在竞争学习中，输出层的神经元相互竞争以便被激活。比赛中获胜的神经元是唯一可以激发的神经元；因此，它被称为“赢家通吃”神经元。在自组织映射中，竞争过程是搜索与输入模式最相似的神经元；获胜者被称为最佳匹配单元（BMU）。

作为获胜标准的相似性可以通过几种方式衡量。最常用的度量指标是欧几里德距离；距离输入信号最短的神经元成为BMU。

在SOM中，学习不仅适用于获胜者，也适用于基于映射的物理上接近它的神经元。BMU享有与其邻近神经元共同学习的特权。邻域的定义由网络设计者确定，最佳接近度取决于其他超参数。如果邻域范围太小，经过训练的模型将遭受过度拟合，并且存在一些死亡神经元的风险，这些神经元永远没有机会改变。

在适应阶段，BMU及其邻近神经元调整其权重。学习的效果是使获胜神经元和相邻神经元的权重更接近输入模式。例如，如果输入信号为蓝色，BMU神经元为浅蓝色，则获胜者的蓝色略高于浅蓝色。如果邻居是黄色的，则会在当前颜色中添加一点蓝色。

概括地讲，自组织映射学习算法（在线学习）可以通过以下4个步骤来描述：

• 初始化

初始化映射层中神经元的权重。

• 竞争过程

选择一个输入样本，并使用距离度量指标在n x m网格中的所有神经元中搜索最佳匹配单元。

• 合作过程

通过邻域函数寻找BMU的邻近神经元。

• 适应过程

通过将数值向输入模式迁移来更新BMU和邻居的权重。

如果达到最大训练迭代次数，则退出；如果还没有，则将迭代计数增加1，并从2开始重复上述过程。

3. 实战演练

在本文中，我们开发的SOM将使用??UCI ML存储网站??上可用的银行票据认证数据集进行训练。该数据文件共包含1372行，每行有4个特征和1个标签。其中，所有4个特征都是不带null的数值；标签是二进制整数值。

首先，我们将数据随机分为训练数据和测试数据。我们使用所有4个特征和在线训练算法来训练自组织映射。然后，我们通过使用训练数据的标签可视化映射来评估经过训练的自组织映射。最后，我们可以基于训练后的映射并使用测试数据来预测标签。

通过这样的实战性演练，我们就可以证明：以无监督方式训练的自组织映射可以用于使用标记数据集的分类。

（1）导入库

import numpy as np
from numpy.ma.core import ceil
from scipy.spatial import distance #距离计算
from sklearn.preprocessing import MinMaxScaler #标准化
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score #评分
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
from matplotlib import animation, colors

（2）导入数据集（dataset）

#钞票认证数据集
# https://archive.ics.uci.edu/ml/datasets/banknote+authentication
# Dua, D. and Graff, C. (2019). UCI机器学习库 [http://archive.ics.uci.edu/ml]. 
# 加州欧文：加利福尼亚大学信息与计算机科学学院。

data_file = "data_banknote_authentication.txt"
data_x = np.loadtxt(data_file, delimiter=",", skiprows=0, usecols=range(0,4) ,dtype=np.float64)
data_y = np.loadtxt(data_file, delimiter=",", skiprows=0, usecols=(4,),dtype=np.int64)

注意，这里的CSV文件需要从网站下载并存储在本地目录中。我们将使用文件中的前4列表示x，最后一列表示y。

（3）训练和测试数据分割

# 训练和测试数据分割
train_x, test_x, train_y, test_y = train_test_split(data_x, data_y, test_size=0.2, random_state=42)
print(train_x.shape, train_y.shape, test_x.shape, test_y.shape) #形状检查

数据按0.8:0.2进行分割，以方便进行训练和测试。因此，我们会看到，分别有1097个和275个观测值。

（4）编写帮助函数

# 帮助函数

# 数据归一化
def minmax_scaler(data):
  scaler = MinMaxScaler()
  scaled = scaler.fit_transform(data)
  return scaled

# 欧几里德距离
def e_distance(x,y):
  return distance.euclidean(x,y)

#曼哈顿距离
def m_distance(x,y):
  return distance.cityblock(x,y)

# 最佳匹配单元搜索
def winning_neuron(data, t, som, num_rows, num_cols):
  winner = [0,0]
  shortest_distance = np.sqrt(data.shape[1]) #用最大距离初始化
  input_data = data[t]
  for row in range(num_rows):
    for col in range(num_cols):
      distance = e_distance(som[row][col], data[t])
      if distance < shortest_distance: 
        shortest_distance = distance
        winner = [row,col]
  return winner

# 学习率和邻域范围计算
def decay(step, max_steps,max_learning_rate,max_m_dsitance):
  coefficient = 1.0 - (np.float64(step)/max_steps)
  learning_rate = coefficient*max_learning_rate
  neighbourhood_range = ceil(coefficient * max_m_dsitance)
  return learning_rate, neighbourhood_range

上述代码中，minmax_scaler用于在0和1之间归一化输入数据。由于算法计算距离，我们应该将每个特征的值缩放到相同的范围，以避免其中任何一个特征对距离计算的影响比其他特征更大。

e_distance变量用于计算两点之间的欧几里德距离。变量m_distance用于获得网格上两点之间的曼哈顿距离。在我们的示例中，欧几里德距离用于搜索获胜神经元，而曼哈顿距离用于限制邻域范围。它通过应用矩形邻域函数简化了计算，其中位于距离BMU拓扑位置一定曼哈顿距离内的神经元在同一级别被激活。

winning_neuron在BMU中搜索样本数据t。计算输入信号与映射层中每个神经元之间的距离，并返回距离最短的神经元网格的行和列索引。

使用当前训练步骤、最大训练步骤数和最大邻域范围和学习速率并应用线性衰减算法，decay函数返回学习速率和邻域范围两个值。

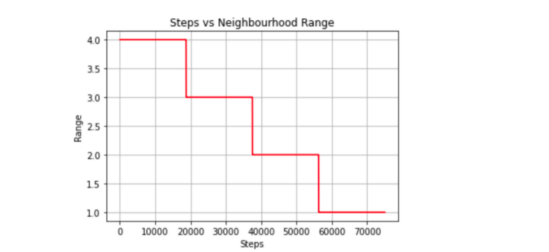
图3-4-1邻域范围衰减情形（步长对邻域范围指标）

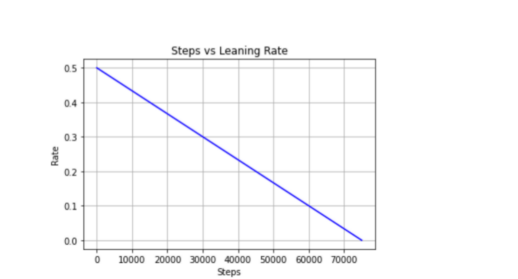
图3-4-2邻域范围衰减（步长对学习速率指标）

（5）设置超参数

# 超参数
num_rows = 10
num_cols = 10
max_m_dsitance = 4
max_learning_rate = 0.5
max_steps = int(7.5*10e3)

# num_nurons = 5*np.sqrt(train_x.shape[0])
# grid_size = ceil(np.sqrt(num_nurons))
# print(grid_size)

超参数是指那些在训练算法之前就需要选择的不可训练参数。它们分别是神经元的数量、SOM网格的维数、训练步骤的数量、学习速率和BMU的邻域范围。

在本例中，我们为网格设置了较小的数字（10×10），但使用了启发式方法来实现超参数选择。我们可以使用[5*sqrt（训练样本数）]公式来选择神经元的数量。我们有1097个训练样本，因此可以在网格上创建5*sqrt（1097）=165.60个神经元（参考文献4）。因为我们有一个二维正方形网格，所以数字的平方根表示每个维度可以有多少个神经元。sqrt的上限（165.40）=13，所以映射的尺寸是13*13。

训练步骤的数量可能需要至少（500×n行×m列）才能收敛。我们可以将步数设置为500*13*13=84500。可以将学习速率和邻域范围设置为较大的数值，并逐渐减小。建议使用不同的超参数集进行实验以进行改进。

最大邻域范围和学习率的初始值可以设置为较大的数字。如果速率太小，可能会导致拟合过度，因此需要更多的学习训练步骤。

（6）开始训练

#主函数

train_x_norm = minmax_scaler(train_x) # 归一化

# 初始wx.qq.com自组织映射
num_dims = train_x_norm.shape[1] # 输入数据的维数
np.random.seed(40)
som = np.random.random_sample(size=(num_rows, num_cols, num_dims)) # 构建映射

#开始训练迭代
for step in range(max_steps):
  if (step+1) % 1000 == 0:
    print("Iteration: ", step+1) # 每1k次打印出当前迭代值
  learning_rate, neighbourhood_range = decay(step, max_steps,max_learning_rate,max_m_dsitance)

  t = np.random.randint(0,high=train_x_norm.shape[0]) # 训练数据的随机索引
  winner = winning_neuron(train_x_norm, t, som, num_rows, num_cols)
  for row in range(num_rows):
    for col in range(num_cols):
      if m_distance([row,col],winner) <= neighbourhood_range:
        som[row][col] += learning_rate*(train_x_norm[t]-som[row][col]) #更新邻接点的权重

print("SOM training completed")

在应用输入数据归一化后，我们使用网格上每个神经元的0到1之间的随机值初始化映射。然后使用衰减函数decay计算学习速率和邻近范围。从训练数据中随机选择样本输入观察值，并搜索最佳匹配单元。最后，基于曼哈顿距离准则，选择包括获胜者在内的邻接点神经元进行学习，并调整权重。

（7）显示训练后的SOM中的标签信息

在上一步中，我们完成了训练。因为这是无监督学习，我们的问题中存在标签数据；所以，我们现在可以将标签投影到映射上。这一步骤是通过两步来实现的。首先，收集每个神经元的标签。其次，将单个标签投影到每个神经元以构建标签映射。

#收集标签

label_data = train_y
map = np.empty(shape=(num_rows, num_cols), dtype=object)

for row in range(num_rows):
  for col in range(num_cols):
    map[row][col] = [] # 置空存储标签的列表

for t in range(train_x_norm.shape[0]):
  if (t+1) % 1000 == 0:
    print("sample data: ", t+1)
  winner = winning_neuron(train_x_norm, t, som, num_rows, num_cols)
  map[winner[0]][winner[1]].append(label_data[t]) # 获胜神经元的标签

上述代码中，我们创建了与SOM相同的网格。对于每个训练数据，我们搜索获胜的神经元，并将观察标签添加到每个BMU的列表中。

# 构建标签映射
label_map = np.zeros(shape=(num_rows, num_cols),dtype=np.int64)
for row in range(num_rows):
  for col in range(num_cols):
    label_list = map[row][col]
    if len(label_list)==0:
      label = 2
    else:
      label = max(label_list, key=label_list.count)
    label_map[row][col] = label

title = ('Iteration ' + str(max_steps))
cmap = colors.ListedColormap(['tab:green', 'tab:red', 'tab:orange'])
plt.imshow(label_map, cmap=cmap)
plt.colorbar()
plt.title(title)
plt.show()

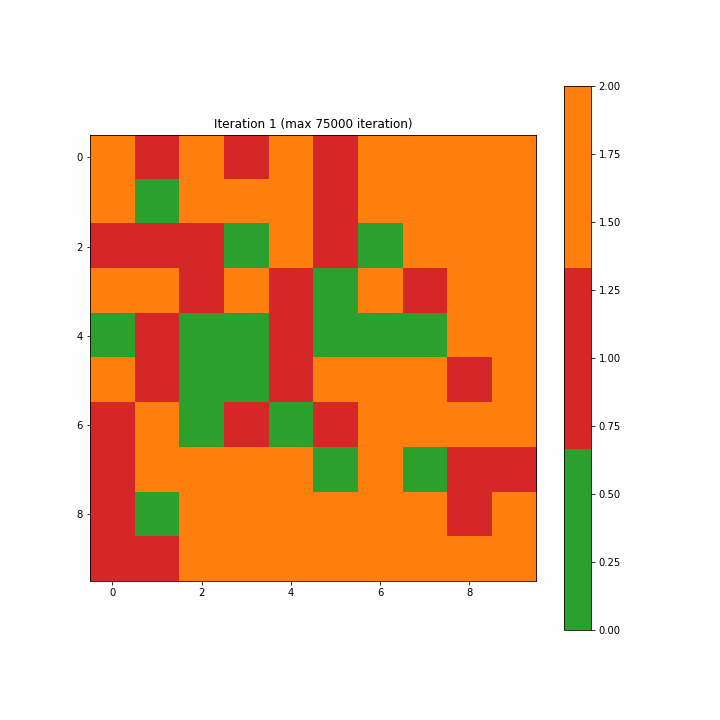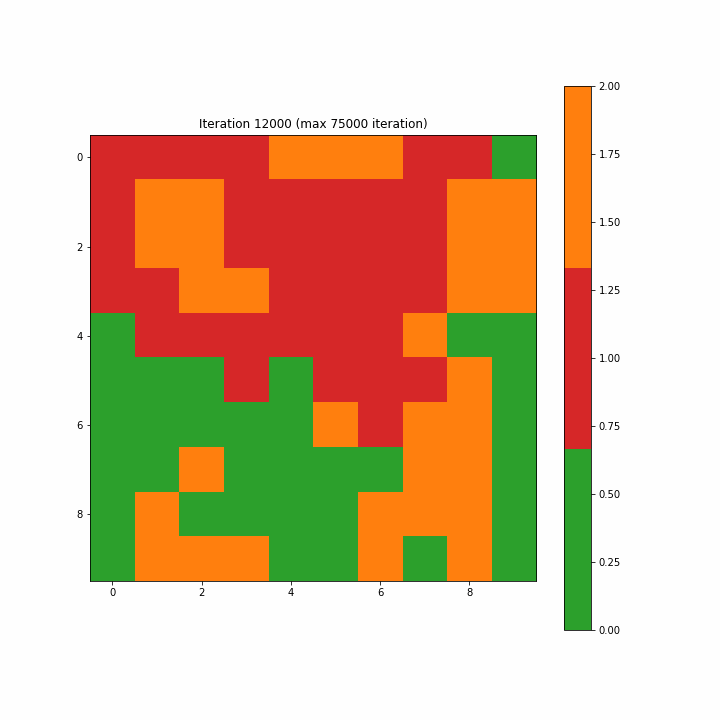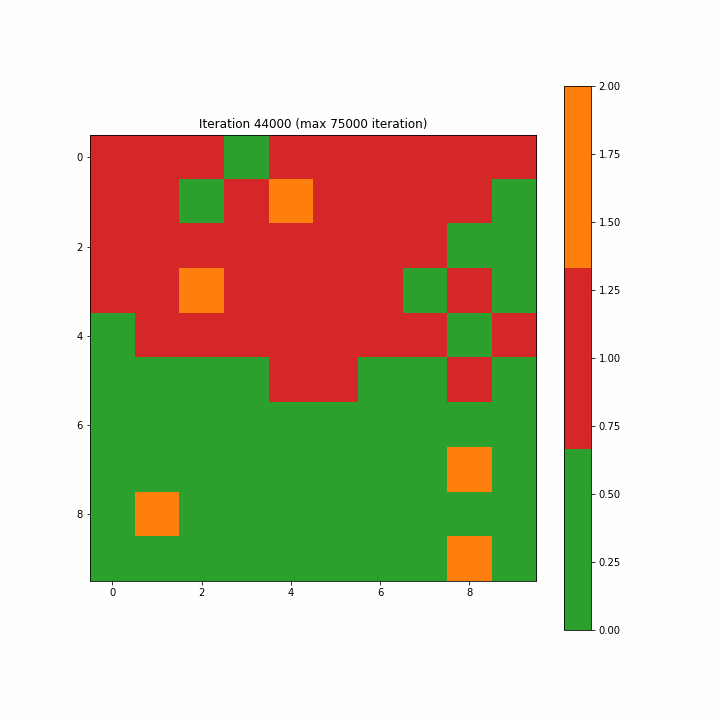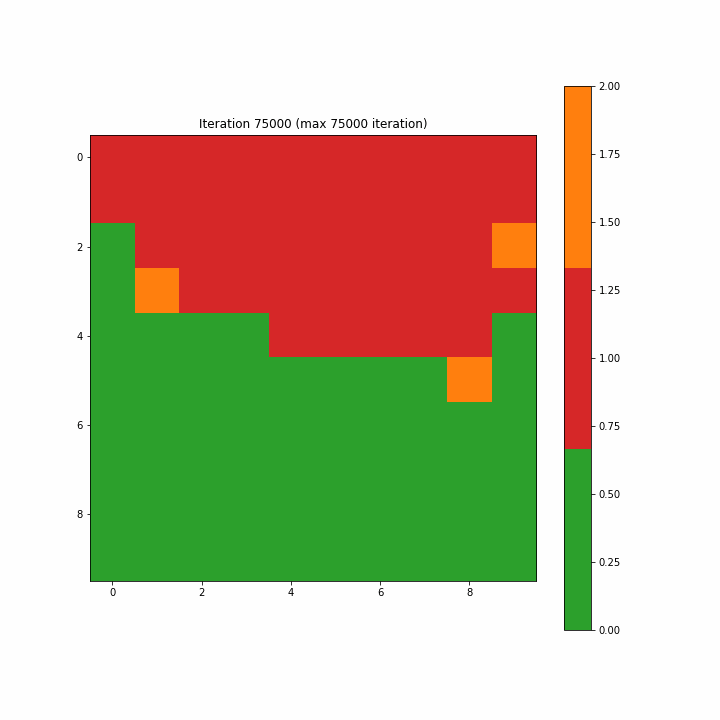
为了构造一个标签映射，我们通过多数投票将单个标签分配给映射上的每个神经元。对于未选择BMU的神经元，我们将类别值2指定为无法识别。图3-7-1和3-7-2分别显示了为第一次迭代和最终迭代创建的标签映射。在开始时，许多神经元既不是0也不是1，分类标签似乎是随机分散的；而最终的迭代清楚地显示了类别0和1之间的区域分离，尽管我们在最终迭代中看到了两个不属于任何一个类别的单元。

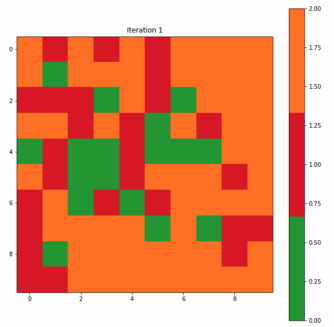
Figure 3–7–1 第一次迭代创建的标签映射

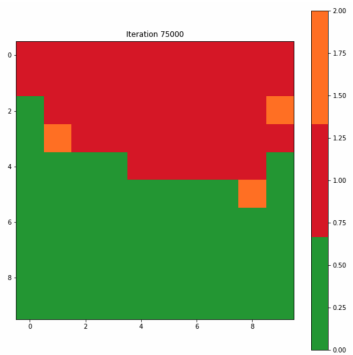
Figure 3–7–2 最终迭代创建的标签映射

注意：如开始的图形一样，原文这里的图3-7-3是一个动画gif，显示了SOM从第一步到最大75000步的演变，方便我们清楚地看到映射的结构。

另外，要生成神经网络训练过程中gif动画的话，您可以参考我上一篇关于使用Matplotlib库对Python片段进行粒子群优化的??文章??。

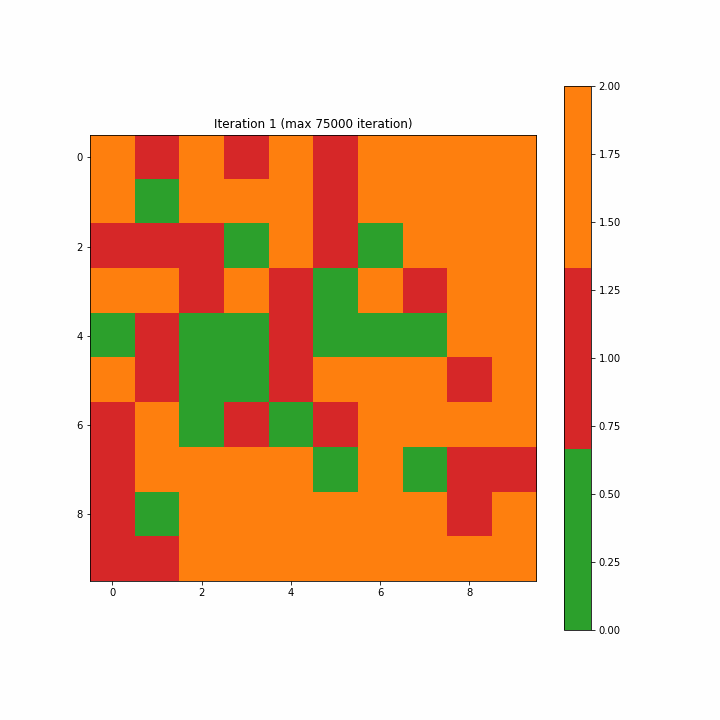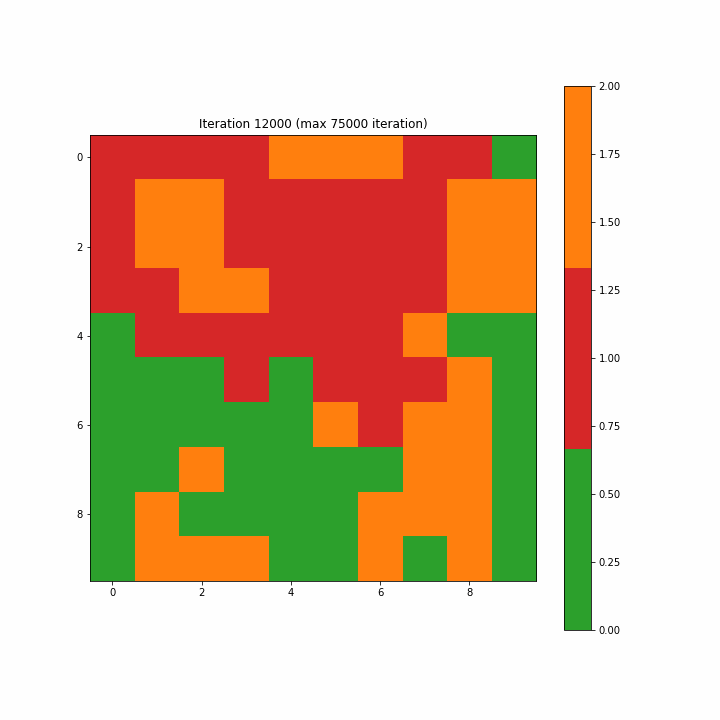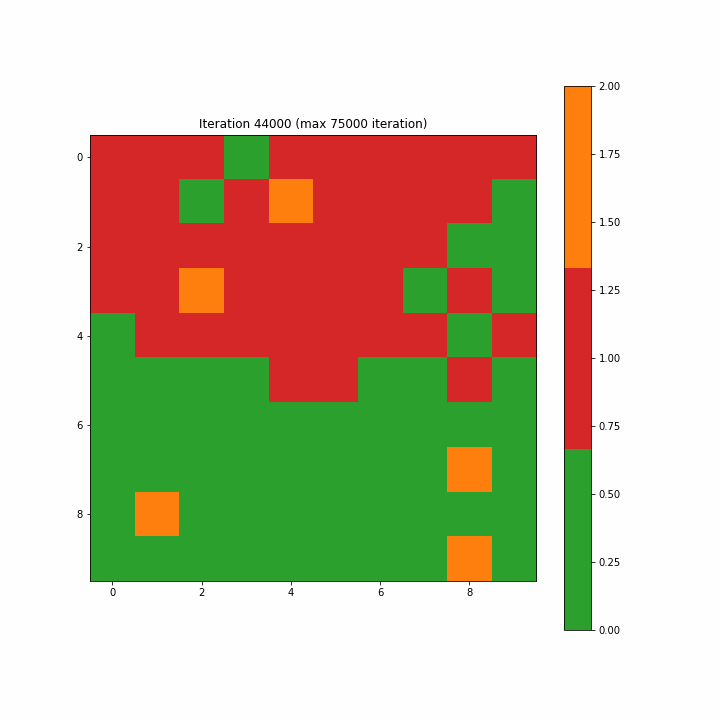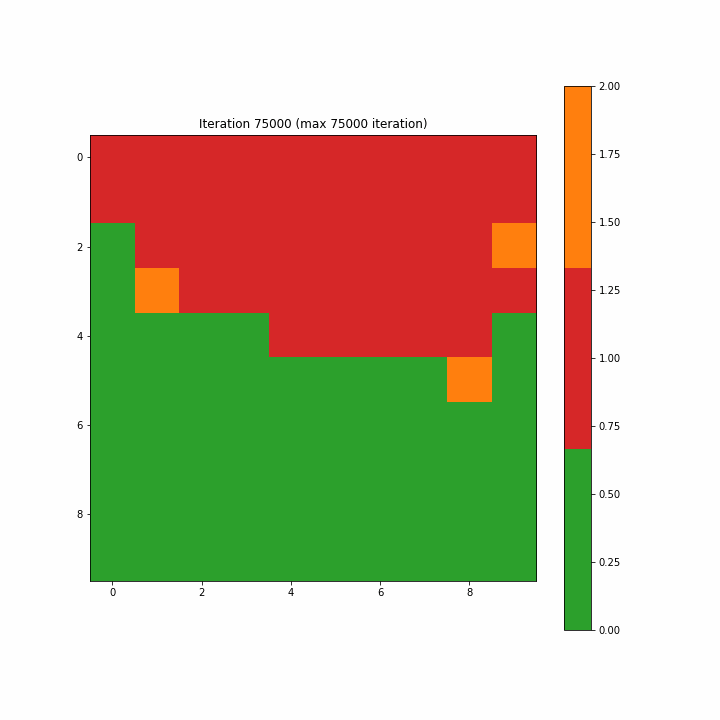
Figure 3–7–3 SOM训练动画

（8）预测测试集标签

#测试数据集

# 利用训练好的自组织映射，搜索测试数据对应的获胜节点，得到获胜节点的标签
data = minmax_scaler(test_x) # normalisation

winner_labels = []

for t in range(data.shape[0]):
 winner = winning_neuron(data, t, som, num_rows, num_cols)
 row = winner[0]
 col = winner[1]
 predicted = label_map[row][col]
 winner_labels.append(predicted)

print("Accuracy: ",accuracy_score(test_y, np.array(winner_labels)))

最后，我们可以使用训练后的映射对测试数据进行二元分类。我们将测试x数据归一化，并搜索每个观察t的MBU，返回与神经元相关的标签。运行结果说明，本训练返回了非常精确的结果，即我们的示例获得了一个非常好的数字，如图3-8所示。

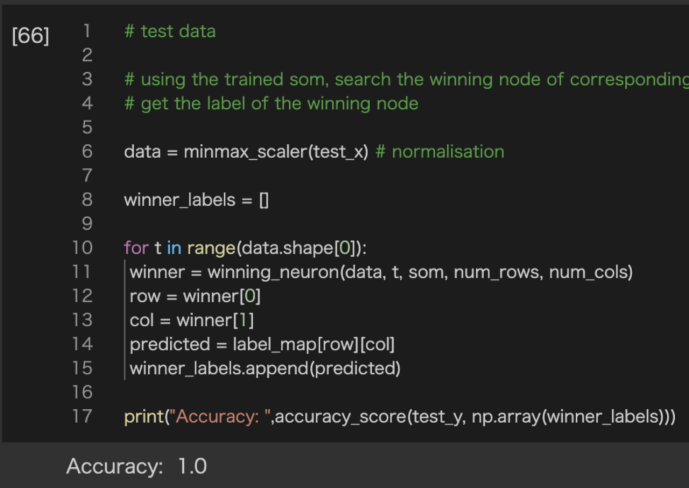
Figure 3–8 预测结果非常理想，精确度为1.0

4. 评估

在上面的示例项目中，我们演示了如何为分类问题实现无监督自组织映射。我们使用没有标签的数据集对映射进行了训练，并通过在映射上投影标签来确认训练结果。正如预期的那样，我们可以观察到每个类别都有清晰的区域，其中神经元具有相似的属性，彼此距离较近。最后，我们用一个不可预见的测试数据集测试了映射，并测量了预测精度。

值得提醒的是，我们用于上述示例的数据仅是一个小而干净的数据集，具有有限的观察值和特征。在现实生活中，数据科学家面临的问题在维度上要高得多，标记的数据集并不完全可用。即使它们可用，其质量也可能不那么完全可靠。例如，在检测银行的恶意交易时，不要期望根据阳性案例检查所有交易，这可能是明智的态度；在真实数据集中，可能只有少数阳性案例被标记。

在将自组织映射应用于真实场景时，我们将面临一些挑战。首先，如果我们没有标记的数据集，我们就无法测量损失。我们无法验证经过训练的映射的可靠性。映射的质量在很大程度上取决于数据本身的特征。归一化数据预处理对于基于距离的算法至关重要。数据集的先验分析对于理解数据点的分布也很重要。特别是对于无法可视化的高维数据，我们可以使用其他降维技术，如主成分分析和奇异值分解（SVD）技术等。

此外，如果拓扑映射的形状与潜在空间中数据点的分布无关，则训练可能不会成功。虽然我们在示例中使用了正方形网格，但我们必须仔细设计映射的形状。推荐的方法之一是使用主成分分析前两个主成分的解释方差的比率。然而，如果时间允许，值得尝试不同的超参数进行精细调整。

就算法的计算成本而言，训练时间复杂度取决于迭代次数、特征数和神经元数。SOM最初是为顺序学习而设计的，但在某些情况下，批量学习方法是首选的。随着大数据的数据量增加，可能有必要研究更有效的学习算法。在我们的示例中，我们使用了称为气泡的矩形邻域函数进行简化。对于训练迭代，我们可以监控自组织映射的形成，并检查在循环过程中如何学习映射。训练步骤数量的减少直接影响计算的数量。

最后需要说明的是，本文中没有介绍批量学习算法有关内容。其实，如果实际问题有关的数据集合比较有限时，则使用批量处理算法是一个不错的选择。事实上，Kohonen指出，批处理算法是有效的，可推荐用于实际应用（见参考文献5）。最后，我们想留下科奥尼撰写的文章“自组织映射要点”的链接（https://www.sciencedirect.com/science/article/pii/S0893608012002596?via%3Dihub）供进一步阅读。

参考文献

[1] T. Kohonen, “Self-organized formation of topologically correct feature maps”, Biological Cybernetics, vol. 43, no. 1, pp. 59–69, 1982, doi: 10.1007/bf00337288.

[2] de Bodt, E., Cottrell, M., Letremy, P. and Verleysen, M., 2004. On the use of self-organizing maps to accelerate vector quantization. Neurocomputing, 56, pp.187–203.

[3] Dua, D. and Graff, C. (2019). UCI Machine Learning Repository [http://archive.ics.uci.edu/ml]. Irvine, CA: University of California, School of Information and Computer Science.

[4] J. Tian, M. H. Azarian, and M. Pecht, “Anomaly Detection Using Self-Organizing Maps-Based K-Nearest Neighbor Algorithm”, PHME_CONF, vol. 2, no. 1, Jul. 2014.

[5] T. Kohonen, “Essentials of the self-organizing map”, Neural Networks, vol. 37, pp. 52–65, Jan. 2013, doi: 10.1016/j.neunet.2012.09.018.

译者介绍

朱先忠，51CTO社区编辑，51CTO专家博客、讲师，潍坊一所高校计算机教师，自由编程界老兵一枚。早期专注各种微软技术（编著成ASP.NET AJX、Cocos 2d-X相关三本技术图书），近十多年投身于开源世界（熟悉流行全栈Web开发技术），了解基于OneNet/AliOS+Arduino/ESP32/树莓派等物联网开发技术与Scala+Hadoop+Spark+Flink等大数据开发技术。

原文标题：??Understanding Self-Organising Map Neural Network with Python Code??，作者：Ken Moriwaki