数字PID温控器7参数辨识和扰动抑制
摘要：结果是STC温控器在热负载扰动下的控制性能大大提升，可与国外知名品牌RKC媲美。
本文引用地址：http://www.eepw.com.cn/article/202205/434588.htm温控器应具备的三个最重要的功能是：能自动辨识控制对象的特征参数（依次表示为KP,、Ti、Td、TR_RM、TD_RM、AMPow和Tp）; 能快速准确辨识扰动源（主要是热负载）大小并及时抑制扰动。而恰在这三功能上，国内市场上一些温控器不尽人意，在大扰动下反应迟钝，偏差大。为此，近一年多来实验室在STC CH902 温控器上创新技术，把扩展继电反馈法[1-2] 和温变速率法成功用在其中。
热容量（用c 表示）和纯延迟时间（用τ 表示）是温控热系统的2 个主要特性参数，但它们又能用上述7参数来反映，这是本辨识温控系统的可行依据。在温控器业界，对PID 三参数的辨识也称为整定。
1? ?温度的PID控制
以纸管干燥机为例，烘房是控制对象；湿的纸管是物料，也可称为热负载，它通过传送带从烘房的一端进，在烘干后从另一端出。以下把热控制系统或温控系统简称为TCS（thermal control system）。
为进行有区别的适应性控制，以热容量为度量可以把温控的全过程划分在4 种状态：空热负载状态（以下简称空载），此时烘房内无纸管（物料）；增加热负载状态（简称加载），此时烘房内从无物料到物料逐渐增多；稳定的热负载状态，此时烘房内的物料量相对稳定；移除热负载状态（简称移载），此时烘房内物料逐渐移出直到空载。后3 种属于热负载变化状态（简称变载）。TCS 的空载状态下的温控是变载状态下温控的基础。
数字离散型PID 闭环控制如图1 所示。
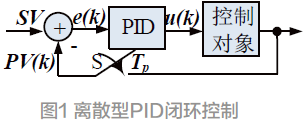
其中SV是设定值；S 是周期为TP的采样开关；PV(k)是过程值PV 的采样值。PID 控制量为：
这是带抗积分饱和的数字PID 差分控制式。结合图1，其中k 和j 是正整数且j<k，是采样序列号；e(k)或e(j) 是对应k or j 时的采样误差，e(k) = SV-PV(k)；[e(k)-e(k-1)] 是一阶后向项差分；u(k) 是与k 对应的控制量，u(k) ∈ [-250,+250]；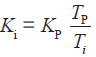
，称为积分系数；
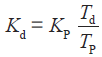，称为微分系数；f(e(k)) 是变速积分系数[4-5]。
温控器最终的控制量输出是由(1) 式的u(k) 转换而来的脉宽调制信号（PWM），用Dr 表示，是信号的占空比。转换公式是：
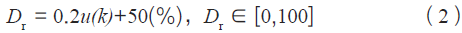
数字PID 温控器一般的温控流程如图2 所示。
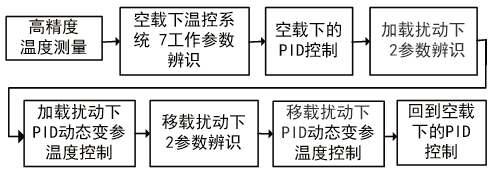
图2 数字PID温控器控温工作流程
相关高精度温度测量的内容详见参考文献[8]。
2? ?参数辨识
辨识包括2 个方面，一是针对在空载状态下TCS的上述7个固有热特征参数；二是针对在变载状态下的扰动源的2个特征性参数。这其中涉及的3个参数要重点说明。
1) 最大降温速率(TD_RM)。这有2 个含义：在空载状态下它是指在图4(a) 的S3 阶段所发生的最大降温速率，用EL_TD_RM 表示；在加载状态下它是指在初始阶段所发生的最大降温速率，用IL_TD_RM 表示，这时，它反映的是扰动源的特性。在工程实践中，它们可用降温1 ℃时所需的最短时间( 秒) 表示。
2) 最大升温速率(TR_RM)。这也有2 个含义：在空载状态下它是指在图4(a) 的S4 和S5 阶段所发生的最大升温速率, 用EL_TR_RM 表示；在移除热负载状态下它是指在初始阶段所发生的最大升温速率, 用RL_TR_RM表示。
这种用TD_RM 和TR_RM 作为辨识扰动源大小量的创新方法称为“温变速率法”。
3) 平均维持功率(AMPow)：它只是空载时的辨识参数，是指图4(a) 中在SV 点附近在一个振荡周期TC内的平均加热功率。这个辨识量对于减少TCS 在受扰动下的调节时间和超调量很有用。在PID 控制开始时AMPow 应作为Dr 的初始功率输出值。
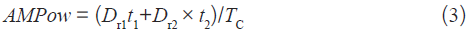
2.1 辨识TCS的7个特性参数
2.1.1 理论基础
7 参数辨识的理论依据是继电反馈法，详见[1-2]。而继电反馈法又是在Z-N（齐格勒- 尼科尔斯）法则[3]上发展起来的。
注意2 点：
1) 理想继电特性的描述函数N(A) 比较特殊，其复角=0，N(A) 由复数退变为实数，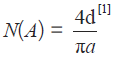
；TCS 的临界振荡增益是Kc，
TC( 或Pu) 是TCS的临界振荡周期( 见图(a）)。
2）如果TC 已确定，则有：KP=0.6 KC，Ti=0.5 TC，Td = 0.12 TC。
2.1.2 理论实现
以实验为例，控温对象是10 公斤重的长形铁块（30 cm×6 cm×6 cm,1340 瓦(PM) 电加热。沿铁块的长度方向均匀分布有14 个测温点，可以模拟实际应用中有不同c 和τ 的TCS，如图3 所示。
图3 温控对象-10公斤的铁块
扩展的继电反馈法原理如图4 所示。
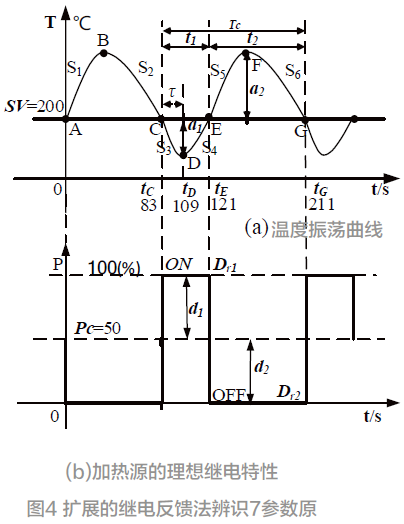
图4(a) 是温度振荡曲线。纵轴是摄氏温度，横轴是时间秒（S），SV 取200 ℃。在图4(a) 中a1、a2 是正负半周的幅值（相对SV 线），a1、a2 ＞ 0；t1、t2 是正负半周期；TC 是周期。大多情况下a1 和a2，t1 和t2 是可以不等的。图4(b) 是与图4(a) 对应的加热源的理想继电特性图，它的纵坐标表示最大加热功率的占空比（P）。图中“ON”表示全功率加温，“OFF”表示关断加热源；PC 是加热功率的中心值[7]（或参考值）, 显然，PC=50(%）；d1 是相对中心值增加的幅值；d2 是相对中心减小的幅值。d1 和d2 象SV, 是必须预先设定好的，d1，d2 ∈ [0,50]，在式(4) 中取d = d1= d2= 50。控制周期Tp 和临界振荡周期TC 二者间的关系，需参考文献[4][6]。辨识结果如表1 所示。
3? ?程序算法与流程
温控器用MCU 是STM32F103，程序开发工具是IAR，语言为C。
3.1 7个TCS特性参数辨识程序
1) 基本要求
如图4(a) 所示， 把整个辨识过程分成6 个阶段（S1 ～ S2），以极值点或交点（温度曲线与SV 线）作为这些阶段分界点（A 点到G 点）；
2）算法
①确认设定值SV( 如200 ℃ )；
②全功率升温至SV；
③如果PV ≥ SV，则停止加热（令Dr = 0）, 进入辨识的阶段1（S1），同时启动定时器（t = tA = 0 秒），tA 是在A 点的时间；
④在S1，要用判断一阶后向差分的符号变化的方法求温度的极大点(B 点)。此点后进入S2；
⑤从S2 开始，记录降温的过程值，以便计算最大降温速率EL_TD_RM；
⑥在S2，如果 PV ≤ SV，则又开始全功率加热（令Dr = 100）升温, 记录tC 并进入S2；
⑦在S3，要开始为计算AMPow 采集数据（Dr 及其持续的时间）直到辨识结束；类似④，要求极小值TD，在D 点后进入S4；
⑧从S4 开始（有些TCS 可能会延长到S5），记录升温的过程值，以便计算最大升温速率EL_TR_RM；
⑨在S4，如果PV ≥ SV，则又停止加热, 记录tE 并进入S5；
⑩在S5，类似④，要求TF，F 点后进入S6；
?在S6，如果PV ≤ SV，记录tG 并进入下列辨识
参数计算：
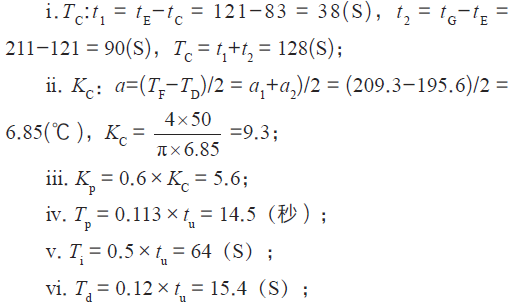
ⅶ. 比较在⑤的记录值, 算得EL_TD_RM = 4（秒/℃）;
ⅷ. 比较在⑧的记录值, 算得EL_TR_RM = 2( 秒/℃ );
ⅸ. 依据（3）式计算AMPow:Dr1 = 100，Dr1 = 0，
AMPow = 28.9（%），
?结束阶段及整个辨识过程。
3.2 扰动源的2个特性参数辨识程序
总体要求有3 个：迅速、准确和稳定可靠，要防止误识别。
1）主要思想
①在主程序中（1 秒钟循环一次），以连续3 次（实验值，可以更多）降温或升温（每次幅度≥ 1 ℃，这里取1 ℃）作为温控状态变化的判断依据。Re 称为速率偏差量（整数），Re ∈ [0,6]；
② PID_Control() 是计算u(k) 和Dr 的函数， 按TP的周期调用。
2）程序流程
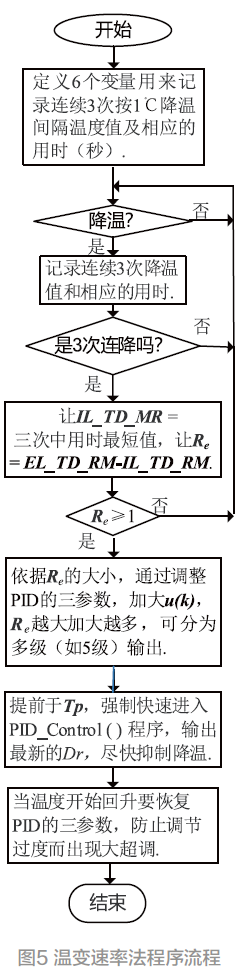
①加载扰动的辨识与抑制的流程见图5。
②移载扰动的辨识与抑制的流程类似图5，只是注意用“升温”及“减小“u(k) 的处理代替图中的“降温”及“加大”u(k) 处理。
4? ?对比测试及数据分析
图6 所示是STC CH902( 左边那一个) 与RKCCH402（日本产知名品牌）二个温控器正在做辨识和抑制热负载扰动性能的对比测试，SV = 200 ℃，以电扇风冷作为加载及移载扰动源。
对比的技术指标及过渡过程如图7 所示。til、Til 是输入加载扰动源时的时间和对应温度；tid、Tid 分别是温控器辨识出加载或移载扰动源及其大小时的时间和温度；tpe、Tpe 是峰值时间和温度；ts、Ts 分别是调节时间（以2%SV 为标准）和温度；tn、Tn 表示由于加载扰动引起TCS 温度迅速下降所达到的负峰值（小于SV）时的时间和温度；T( ∞ ) 是稳态值；tss、Tss 分别是指抑制扰动后TCS 重新进入到稳态的第一时间和温度，稳态误差ess = SV-T( ∞ ) ≈ SV-Tss，这里Tss ∈ [199.4,200.6]，ess ∈[-0.6,0.6]。
注意几点：
①图中时间t 的单位是秒（S），温度T 的单位是℃；
②负峰值只在稳态时间前出现才有效，有时可能没有，如图7(b) 所示；
图6 STC和RKC性能对比测试
③做加载扰动时把til的时间设为0 点，其它时间指标是相对此点而言；类似，在移载扰动时把trl 的时间设为0 点，如图7 所示。
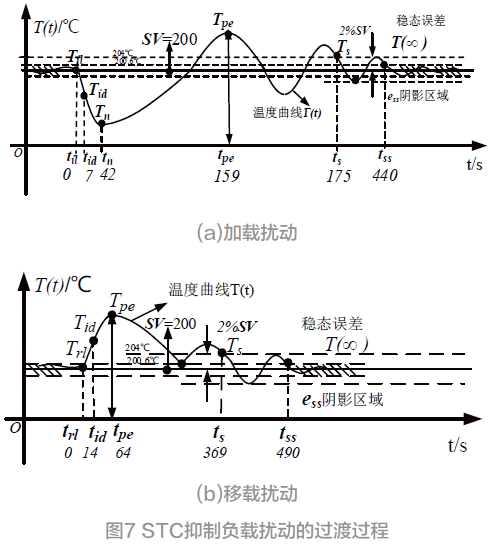
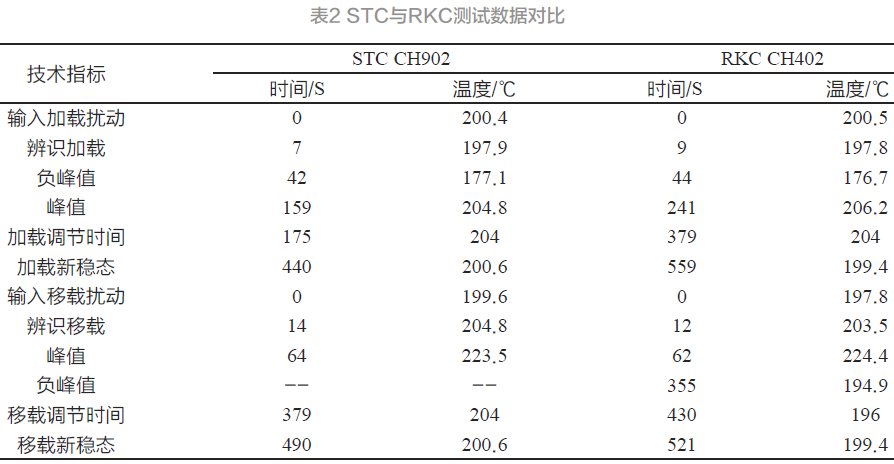
表2 中各项技术指标值即是对应的时间和温度。
表中“--”表示无负峰值出现。
在表2 中能看到STC CH902 和RKC CH402 在辨识热负载方面有相近的性能（看指标的第2、3 及8、9 项），且二者都达到200±0.6 ℃的稳态误差。但在抑制负载扰动方面STC 更有效，不仅峰值更低和负峰值更高，而且调节时间及进入新的高精度稳态的时间要更短（看指标的第4~6，10~12 项）。
5? ?结论
表2 的数据表明扩展的继电反馈法和温变速率法的结合应用能有效提升温控器在辨识和抑制扰动方面的控制性能。例如，在强风冷却扰动下最大偏差（降温时）、超调量及调节时间比之前分别减少9 ℃、3 ℃和6 分钟，稳态误差则同RKC。
参考文献：
[1] ASTR?M K J,H?GGLUND Automatic tuning of simple regulators with specifications on phase and amplitude margins
[J],Automatica,1984,20(5):645-651.
[2] ASTR?M K J.Adaptation,auto-tuning and smart controls[M/OL]//Technical Reports TFRT-7340,Department of Automatic Control,Lund Institute of Technology,1987:430-431.https://?lup.lub.lu.se/record/8602272.
[3] ZIEGLER J G,NICHOLS N B.,Optimum setting for automatic controllers,trans[J].ASME,1942,64:759-768.
[4] 潘新民.微型计算机控制技术[M].2版.北京:人民邮电出版社,1988:220-239.
[5] 苏绍兴.基于变速积分PID的温度控制系统的设计[J].机电工程,2002,19(6):28.
[6] BUCZ ?,KOZáKOVá A.PID controller design for specified performance[M].Slovak Republic,2012.
[7] 殷华文.温度控制继电反馈参数自整定技术研究[J].自动化仪表,2016.37(3):23-26.
[8] 王昌世.数字温控器高精度测温设计[J].电子产品世界,2021,28(8):60-66,73.
（本文来源于《电子产品世界》杂志2022年5月期）
