数学之美：谈Smith圆图

　　Smith Chart对于一个射频工程师而言是一个非常重要的辅助工具。笔者N年前学习圆图的时候，对于圆图仅仅是一种感性和浅显的认识，纯粹为了考试而去学习圆图。比如圆图上某个点为开路点，某个点为短路点，某个点反射系数最大，某个点反射系数为0等等。圆图丢了N年，此次重新捡起来，重新学习，又感觉对圆图的理解还是不够深入，而且感觉圆图背后还有许多没有被自己所理解的信息，因此，目前还是处于一知半解的程度。

　　近日在网上搜罗关于圆图的相关知识，重新学习，将自己目前对圆图的理解在此作为一个总结。

　　1、Smith Chart是用来协助解决传输线问题和匹配问题的一个工具。

　　日常大家所见到的二维圆图仅仅可以用来解决常规射频电路的匹配问题，亦即阻抗实部为正的问题。近日在IEEE MTT论坛中，一个老外又提出了广义Smith Chart的概念，可以用来解决阻抗实部为负的的匹配问题，比如射频振荡器。

　　2、Smith Chart上可以反映出如下信息：

　　阻抗参数Z，导纳参数Y，品质因子Q，反射系数，驻波系数，Snn散射参数，噪声系数，增益，稳定因子，功率，效率，频率信息等。

　　相对应上述参数信息，Smith Chart上面分别对应着一系列circle或者contour 。

　　3、Smith Chart上面的圆周刻度

　　波长刻度：用来表示传输线和负载之间的传输线的长度信息，通常用来解决分布参数问题。

　　角度数：用来表示以极坐标形式表示的反射系数的角度信息。

　　4、通常我们的求解过程都是通过Smith Chart上面一系列点来完成的，每一个点对应一个频点和该频点下的阻抗或者导纳。匹配的过程最终都是将起点通过旋转和单位电抗圆或者单位电纳圆相交，然后回到圆心，完成匹配过程。

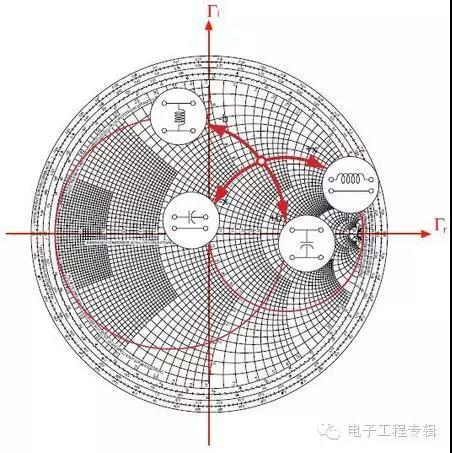
　　5、窄带匹配和宽带匹配

　　通常在圆图上面单点完成匹配，对于窄带应用而言已经够用。但是对于宽带而言，需要将这些匹配点最终连接起来，确保这些点的轨迹在宽带频段覆盖范围之内，或者在某一个参数指标圆内，比如VSWR=1.3的驻波圆。

　　6、传统的2维Smith Chart的局限性。

　　当阻抗的实部为负数的时候，2维Smith Chart就无法表示该阻抗值，相应的一系列参数也无法在圆图上体现出来，尤其是在处理振荡器的时候，阻抗的实部往往就是一个负数。对此英国一个叫Chris Zelley的人，提出用三维球面来解决，并提出了他的设想，如下图所示

　　我想这是一个很具有创意的设想。尤其是当这个想法的可操作性得到进一步证实，并经过理论的验证之后，一个像地理课上地球仪一样的3维Smith Sphere也会放在射频或者微波课的讲桌上。

　　当年，贝尔试验室的Smith将传输线问题的求解通过一张图表来直观化，而今又是一名英国的工程师将传输线问题进一步通过三维球面来进一步推广，将Smith Chart推广到更为普遍的一种情形。

　　7、Smith Chart是通过两个复数域内的变量--阻抗和反射系数的关系推导而来，其他参数或者系列参数圆也是通过这种变换可以得到。

　　8、Smith Chart上面的源(Source)和负载(Load)之间是相对的，既可以将源当作负载，也可以将负载当作源来处理，因为无论是源或者负载，最终在圆图上都表现为阻抗，因此具有相对性。

　　9、针对端接负载ZL的有损(lossy)传输线而言，其在Smith Chart上面反射系数是一个顺时针向内旋转的螺旋，如果传输线比较长，那么这个螺旋最终会终止于Smith Chart的圆心。

　　那么根据反射系数与驻波系数的关系可以推出，端接负载ZL的有损传输线上的驻波系数是一个顺时针向外旋转的螺旋，如果传输线足够长，最终会终止于VSWR=1的驻波圆上。如下图所示

　　又是数学，感觉数学无处不在，作为一个射频工程师，数学功底会决定他对理论的掌握程度，并进而影响他在工程实践中提高的快慢。

　　不禁感慨，数学还需要进一步学习。